题目内容
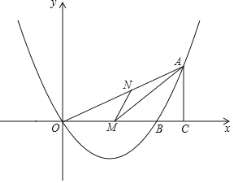
【题目】如图所示，抛物线
与
轴交于A、B两点，与
轴交于点C，直线
经过A、C两点．
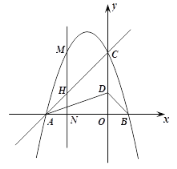
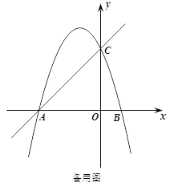
（1）求抛物线的解析式；
（2）点N是轴上的动点，过点N作轴的垂线，交抛物线与点M，交直线AC于点H．
①点D在线段OC上，连结AD、BD，当
时，求
的最小值；
②当
时，将直线AD绕点A旋转
，使直线AD与轴交于点P，请直接写出点P的坐标．
【答案】（1）抛物线的解析式为
；（2）①
的最小值为4；②点P的坐标为
或
．
【解析】
（1）先根据直线的解析式求出点A、C的坐标，再利用待定系数法求解即可得；
（2）①先根据抛物线的解析式求出点B的坐标，从而可得AB的长，再根据等量代换、两点之间线段最短即可得出答案；
②如图（见解析），分两种情况讨论：先根据点A、B坐标、等腰直角三角形的判定与性质得出DE、AE、OA的长，再根据相似三角形的判定与性质可得出OP的长，从而可得点P的坐标．
（1）对于
，令
得
，令
得
，解得
∴
把点代入
得
解得
则抛物线的解析式为；
（2）①令
解得
∴
∵
∴
由两点之间线段最短可知，
的最小值为AB
即的最小值为4；
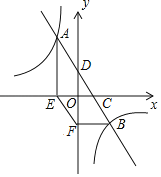
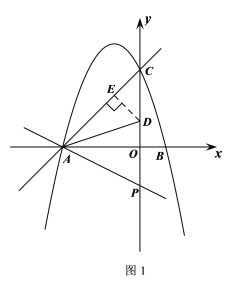
②由题意，分以下两种情况：
如图1，当直线AD绕点A顺时针旋转
时，
∵
∴
为等腰直角三角形
∴
作
，则
为等腰直角三角形
∵
∴
在
中，
∴
在
和
中，
∴
，即
解得
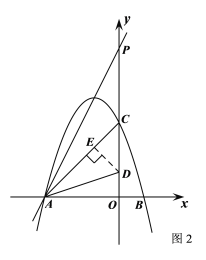
如图2，当直线AD绕点A逆时针旋转时，
∵
∴
作
在和
中，
∴
，即
解得
综上，点P的坐标为或．
练习册系列答案
阅读快车系列答案
相关题目
