题目内容
3.用配方法解下列方程:(1)2x2-4x-1=0;
(2)2x2+7x-1=19-x2.
分析 (1)先把方程两边都除以2,使二次项的系数为1,然后再配上一次项系数一半的平方;
(2)先把方程两边都除以2,使二次项的系数为1,然后再配上一次项系数一半的平方.
解答 解:(1)移项得,2x2-4x=1,
二次项系数化成1得,x2-2x=$\frac{1}{2}$,
配方得,x2-2x+1=$\frac{1}{2}$+1,
即(x-1)2=$\frac{3}{2}$,
开方得,x-1=±$\frac{\sqrt{6}}{2}$,
所以,x1=1+$\frac{\sqrt{6}}{2}$,x2=1-$\frac{\sqrt{6}}{2}$;
(2)整理得,3x2+7x=20,
二次项系数化成1得,x2+$\frac{7}{3}$x=$\frac{20}{3}$,
配方得,x2+$\frac{7}{3}$x+$\frac{49}{36}$=$\frac{20}{3}$+$\frac{49}{36}$,
即(x+$\frac{7}{6}$)2=$\frac{289}{36}$,
开方得,x+$\frac{7}{6}$=±$\frac{17}{6}$,
所以,x1=4,x2=-$\frac{5}{3}$.
点评 本题考查了配方法解方程.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.已知Rt△ABC中,∠A=90°,∠B=30°,CD平分∠ACB且与AB边交于点D,AC=$\sqrt{6}$,则点D到边BC的距离是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
14.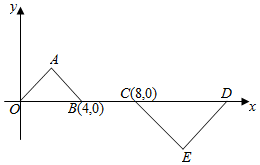 如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
 如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
12.当b<0时,一次函数y=2x+b的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
 如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.
如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.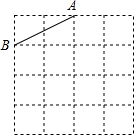 已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题:
已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题: