题目内容
17.先化简,再求值:(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$,其中x=-2.分析 首先将括号里面通分,进而分解因式化简求出即可.
解答 解:(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$,
=$\frac{x-2}{x-1}$×$\frac{(x-1)(x+1)}{(x-2)^{2}}$
=$\frac{x+1}{x-2}$,
将x=-2代入得:原式=$\frac{-2+1}{-2-2}$=$\frac{1}{4}$.
点评 此题主要考查了分式的化简求值,正确因式分解得出是解题关键.

练习册系列答案
相关题目
9.二次函数y=kx2-6x+3的图象与x轴有两个交点,则k的取值范围是( )
| A. | k<3 | B. | k<3且k≠0 | C. | k≤3 | D. | k≤3且k≠0 |
6. 如图,已知F是以AC为直径的半圆O上任一点,过AC上任一点H作AC的垂线分别交CF、AF的延长线于点E、B,DB=DE.
如图,已知F是以AC为直径的半圆O上任一点,过AC上任一点H作AC的垂线分别交CF、AF的延长线于点E、B,DB=DE.
(1)求证:DF是⊙O的切线;
(2)若BF=AF,求证:AF2=EF•CF.
 如图,已知F是以AC为直径的半圆O上任一点,过AC上任一点H作AC的垂线分别交CF、AF的延长线于点E、B,DB=DE.
如图,已知F是以AC为直径的半圆O上任一点,过AC上任一点H作AC的垂线分别交CF、AF的延长线于点E、B,DB=DE.(1)求证:DF是⊙O的切线;
(2)若BF=AF,求证:AF2=EF•CF.
7.2的平方根为( )
| A. | 4 | B. | ±4 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |

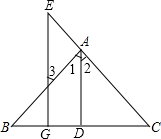 如图,在△ABC中,E是CA延长线上一点,AD⊥BC于D,EG⊥BC于G,∠E=∠3.
如图,在△ABC中,E是CA延长线上一点,AD⊥BC于D,EG⊥BC于G,∠E=∠3.