题目内容
9．二次函数y=kx2-6x+3的图象与x轴有两个交点，则k的取值范围是（ ）| A． | k＜3 | B． | k＜3且k≠0 | C． | k≤3 | D． | k≤3且k≠0 |
分析 根据根的判别式与二次函数的定义列出关于k的不等式组，求出k的取值范围即可．
解答 解：∵二次函数y=kx2-6x+3的图象与x轴有两个交点，
∴$\left\{\begin{array}{l}△＞0\\ k≠0\end{array}\right.$，即$\left\{\begin{array}{l}△=36-12k＞0\\ k≠0\end{array}\right.$，
解得k＜3且k≠0．
故选B．
点评 本题考查的是抛物线与x轴的交点，熟知抛物线与x轴的交点与△的关系是解答此题的关键．
练习册系列答案
相关题目
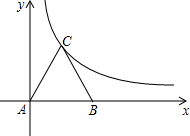如图，等边△ABC放置在平面直角坐标系中，已知A（0，0）、B（2，0），反比例函数的图象经过点C．