题目内容
 如图,等腰△ABC中,AB=AC,BC=10,角平分线AD=12,点E是AC中点,求DE的长.
如图,等腰△ABC中,AB=AC,BC=10,角平分线AD=12,点E是AC中点,求DE的长.考点:勾股定理,等腰三角形的性质,直角三角形斜边上的中线
专题:
分析:根据等腰三角形的三线合一的性质,得到AD是等腰△ABC底边BC上的高,然后根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长.
解答:解:∵AB=AC,AD 是角平分线,
∴AD⊥BC,且DC=
BC=5,
∵AD=12,
∴在Rt△ACD中,由勾股定理得:
AC=
=13,
∵点E是AC中点
∴DE=
AC=
.
∴AD⊥BC,且DC=
| 1 |
| 2 |
∵AD=12,
∴在Rt△ACD中,由勾股定理得:
AC=
| 52+122 |
∵点E是AC中点
∴DE=
| 1 |
| 2 |
| 13 |
| 2 |
点评:本题考查了等腰三角形的性质以及直角三角形斜边上的中线的性质,解题的根据是熟练运用等腰三角形的性质.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
如果a+b>0,且ab<0,那么下列结论正确的是( )
| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a,b异号且正数的绝对值较小 |
| D、a,b异号且负数的绝对值较小 |
下列运算中,正确的是( )
| A、a2•a3=a6 |
| B、(a3)3=a9 |
| C、(2a2)2=2a4 |
| D、a9÷a2=a4 |
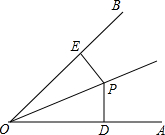 如图,∠POB=∠POA,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠POB=∠POA,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )| A、PD=PE |
| B、OD=OE |
| C、PD=OD |
| D、∠DPO=∠EPO |