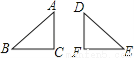
��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��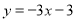 ��x�ύ�ڵ�A����y�ύ�ڵ�C.������
��x�ύ�ڵ�A����y�ύ�ڵ�C.������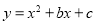 ����A��C���㣬����x�ύ����һ��B����B�ڵ�A�Ҳࣩ��
����A��C���㣬����x�ύ����һ��B����B�ڵ�A�Ҳࣩ��
��1���������ߵĽ���ʽ����B���ꣻ
��2������M���߶�BC�ϵ�һ���㣬����M��ֱ��EFƽ��y�ύx���ڵ�F�����������ڵ�E.��ME�������ֵ��
��3����̽����MEȡ���ֵʱ�����������ϡ�x���·��Ƿ���ڵ�P��ʹ��M��F��B��PΪ������ı�����ƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
������ �������� �����������1���������A,C�����꣬Ȼ����룬�ⷽ���鼴�ɣ���2�����ֱ��BC�Ľ���ʽ��y��x��3�����ݵ�M��ֱ��BC �ϣ���M��x��x��3������E��x��x2��2x��3�� ����ʾ���߶�ME�ij������䷽����������ֵ����3������������x���·����ڵ�P��ʹ��P��M��F��BΪ������ı�����ƽ���ı��Σ������P�����꣬Ȼ���жϵ�P�Dz������������ϼ���. �������...
��ϰ��ϵ�д�
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
�����Ŀ


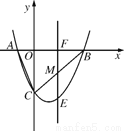
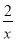 �ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B������A��y��Ĵ��ߣ�����B��x��Ĵ��ߣ������߽��ڵ�C�����ŵ�A���˶�����C��λ��Ҳ��֮�仯�����C������Ϊ(m��n)����m��n����Ĺ�ϵʽΪ( )
�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B������A��y��Ĵ��ߣ�����B��x��Ĵ��ߣ������߽��ڵ�C�����ŵ�A���˶�����C��λ��Ҳ��֮�仯�����C������Ϊ(m��n)����m��n����Ĺ�ϵʽΪ( )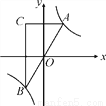
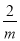 C. n����4m D. n����
C. n����4m D. n����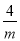
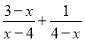 =1
=1 B.
B. 
 D.
D.