题目内容
(1)已知2a-1的平方根是±3,3a+2b+4的立方根是3,求a+b的平方根.
(2)若|m+n-5|+(2m+3n-5)2=0,求(m-n)2的值.
(2)若|m+n-5|+(2m+3n-5)2=0,求(m-n)2的值.
考点:立方根,非负数的性质:绝对值,非负数的性质:偶次方,平方根,解二元一次方程组
专题:计算题
分析:(1)利用平方根及立方根定义求出a与b的值,即可确定出a+b的平方根;
(2)利用非负数的性质求出m与n的值,代入原式计算即可得到结果.
(2)利用非负数的性质求出m与n的值,代入原式计算即可得到结果.
解答:
解:(1)∵2a-1的平方根是±3,3a+2b+4的立方根是3,
∴
,
解得:
,
则a+b=9,9的平方根为±3;
(2)∵|m+n-5|+(2m+3n-5)2=0,
∴
,
解得:
,
则(m-n)2=225.
∴
|
解得:
|
则a+b=9,9的平方根为±3;
(2)∵|m+n-5|+(2m+3n-5)2=0,
∴
|
解得:
|
则(m-n)2=225.
点评:此题考查了立方根,非负数的性质,平方根,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
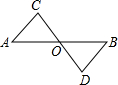 如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论:
如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论: