题目内容
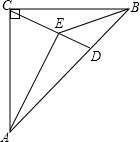 在△ABC中,∠ACB=90°,AC=BC,点D在AB边上,点E在线段CD上,∠AEB=135°,若AD=4,BD=2,则线段CE的长为
在△ABC中,∠ACB=90°,AC=BC,点D在AB边上,点E在线段CD上,∠AEB=135°,若AD=4,BD=2,则线段CE的长为考点:圆的综合题
专题:
分析:作△AEB的外接圆⊙O,延长CD交⊙O于点F,连接AO并延长交⊙O于点F',连接CF'交AB于D',连接AF,BF,OB,如图.根据圆内接四边形的性质可得∠AFB=45°,根据圆周角定理可得∠AOB=90°,进而可证到四边形ACBO是正方形,然后利用相似三角形的性质可得AB=3BD′.由条件可知AB=3BD,故点D'与点D重合,则点F'与点F重合,因而AF是⊙O的直径,则有AE⊥CF,从而可证到△CEA∽△CAF,就可得到CE=
,只需利用三角函数及勾股定理就可求出CA、CF进而求出CE.
| CA2 |
| CF |
解答:解:作△AEB的外接圆⊙O,延长CD交⊙O于点F,
连接AO并延长交⊙O于点F',连接CF'交AB于D',
连接AF,BF,OB,如图.
∵∠AEB=135°,∴∠AFB=45°,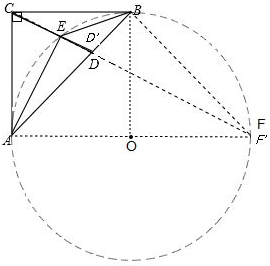
∴∠AOB=2∠AFB=90°,
∵OA=OB,∴∠OAB=∠OBA=45°.
∵∠ACB=90°,AC=BC,
∴∠ABC=∠CAB=45°,
∴∠CBO=∠CAO=90°,
∴∠CBO=∠CAO=∠ACB=90°,
∴四边形ACBO是矩形.
∵OA=OB,∴矩形ACBO是正方形,
∴BC∥AO,CA=AO=BC即AF'=2BC.
∴△AF'D'∽△BD'C.
∴
=
=2.
∴AD'=2BD′.
∴AB=3BD′.
∵AD=4,BD=2,∴AB=6=3BD,
∴BD′=BD,
∴点D'与点D重合,
∴点F'与点F重合,
∴AF是⊙O的直径,
∴AE⊥CF,
∴∠CEA=∠CAF=90°.
∵∠ECA=∠ACF,
∴△CEA∽△CAF,
∴
=
,即CE=
.
∵AD=4,BD=2,∴AB=6,
∴AC=AB•sin45°=6×
=3
,
∴AB=2AC=6
,
∴CF=
=3
,
∴CE=
=
=
.
故答案为:
.
连接AO并延长交⊙O于点F',连接CF'交AB于D',
连接AF,BF,OB,如图.
∵∠AEB=135°,∴∠AFB=45°,

∴∠AOB=2∠AFB=90°,
∵OA=OB,∴∠OAB=∠OBA=45°.
∵∠ACB=90°,AC=BC,
∴∠ABC=∠CAB=45°,
∴∠CBO=∠CAO=90°,
∴∠CBO=∠CAO=∠ACB=90°,
∴四边形ACBO是矩形.
∵OA=OB,∴矩形ACBO是正方形,
∴BC∥AO,CA=AO=BC即AF'=2BC.
∴△AF'D'∽△BD'C.
∴
| AD′ |
| BD′ |
| AF′ |
| BC |
∴AD'=2BD′.
∴AB=3BD′.
∵AD=4,BD=2,∴AB=6=3BD,
∴BD′=BD,
∴点D'与点D重合,
∴点F'与点F重合,
∴AF是⊙O的直径,
∴AE⊥CF,
∴∠CEA=∠CAF=90°.
∵∠ECA=∠ACF,
∴△CEA∽△CAF,
∴
| CA |
| CF |
| CE |
| CA |
| CA2 |
| CF |
∵AD=4,BD=2,∴AB=6,
∴AC=AB•sin45°=6×
| ||
| 2 |
| 2 |
∴AB=2AC=6
| 2 |
∴CF=
| CA2+AB2 |
| 10 |
∴CE=
| CA2 |
| CF |
| 18 | ||
3
|
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:本题主要考查了圆内接四边形的性质、圆周角定理、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识,构造辅助圆是解决本题的关键,运用同一法证到AF是⊙O的直径又是解决本题过程中的一个难点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
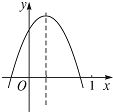 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②方程ax2+bx+c=0的两根之和大于0;③2a+b>0;④a-b+c<0,其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②方程ax2+bx+c=0的两根之和大于0;③2a+b>0;④a-b+c<0,其中正确的个数( )| A、4个 | B、3个 | C、2个 | D、1个 |
若a>b,则下列各式中必成立的是( )
| A、ma>mb |
| B、b-a<0 |
| C、a2>b2 |
| D、1-a>1-b |