题目内容
14. 如图,?ABCD的周长为36,对角线AC、BD相交于点O.点E是CD的中点,BD=14,则△DOE的周长为( )
如图,?ABCD的周长为36,对角线AC、BD相交于点O.点E是CD的中点,BD=14,则△DOE的周长为( )| A. | 50 | B. | 32 | C. | 16 | D. | 9 |
分析 由平行四边形的性质和已知条件得出OD=7,CD+BC=18,再证明OE是△BCD的中位线,得出DE+OE=9,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD=$\frac{1}{2}$BD=7,
∵?ABCD的周长为36,
∴CD+BC=18,
∵点E是CD的中点,
∴DE=$\frac{1}{2}$CD,OE是△BCD的中位线,
∴OE=$\frac{1}{2}$BC,
∴DE+OE=$\frac{1}{2}$(CD+BC)=9,
∴△DOE的周长=OD+DE+OE=7+9=16;
故选:C.
点评 本题考查了平行四边形的性质、三角形中位线定理;熟练掌握平行四边形的性质,运用三角形中位线定理是解决问题的关键.

练习册系列答案
相关题目
4.某商店销售一种玩具,每件售价90元,可获利15%,求这种玩具的成本价.设这种玩具的成本价为x元,依题意列方程,正确的是( )
| A. | $\frac{90-x}{x}$=15% | B. | $\frac{90}{x}$=15% | C. | 90-x=15% | D. | x=90×15% |
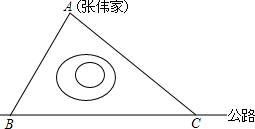 张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离.
张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离. 如图为某地下停车库的出入口坡道示意图,其中AB∥MN,BD⊥AB,CE⊥AM.为张贴限高标志以确保车辆安全驶入,请你根据该图提供的数据计算CE.(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325,答案精确到0.1m)
如图为某地下停车库的出入口坡道示意图,其中AB∥MN,BD⊥AB,CE⊥AM.为张贴限高标志以确保车辆安全驶入,请你根据该图提供的数据计算CE.(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325,答案精确到0.1m) 如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.