题目内容
12.解方程(1)$\frac{3-x}{x-4}$+$\frac{1}{4-x}$=1
(2)$\frac{2x+2}{x}$-$\frac{x}{x-2}$=$\frac{{x}^{2}-2}{{x}^{2}-2x}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:3-x-1=x-4,
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:2x2-2x-4-x2=x2-2,
解得:x=-1,
经检验x=-1是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
18. 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )| A. | ED=CD | B. | AD=BD | C. | AB=AC | D. | BD=AC |
16.在下列特征中,菱形具有而平行四边形不一定具有的是( )
| A. | 内角和等于360° | B. | 对角相等 | ||
| C. | 每条对角线平分一组对角 | D. | 邻角互补 |
7.观察如图给出的四个点阵,S表示每个点阵中的点的个数,按照图形中点的个数变化规律,则第8个点阵中的点的个数是( )
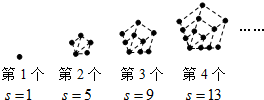

| A. | 29 | B. | 25 | C. | 24 | D. | 22 |
1.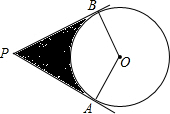 如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )
如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )
 如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )
如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )| A. | 12$\sqrt{3}$-4π | B. | 24$\sqrt{3}$-4π | C. | 12$\sqrt{3}$-2π | D. | 24$\sqrt{3}$-2π |
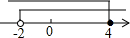
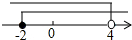


 如图,直线y=x+m(m>0)与x轴交于点A(-2,0),与y轴交于点E,直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=x+m(m>0)相交于点D,若AB=3,
如图,直线y=x+m(m>0)与x轴交于点A(-2,0),与y轴交于点E,直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=x+m(m>0)相交于点D,若AB=3, 将一副标准的直角三角尺如图放置,已知AE∥BC,求∠AFD的度数.
将一副标准的直角三角尺如图放置,已知AE∥BC,求∠AFD的度数.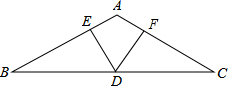 如图,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为E,F,∠BAC=120°,BC=12,求DE+DF的值.
如图,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为E,F,∠BAC=120°,BC=12,求DE+DF的值.