题目内容
8.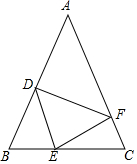 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
分析 (1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质得到∠CEF=∠BDE,于是得到∠DEF=∠B,根据等腰三角形的性质即可得到结论.
(3)由(1)知:△DEF是等腰三角形,DE=EF,由(2)知,∠DEF=∠B,于是得到结论.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵$\left\{\begin{array}{l}{BE=CF}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△BDE≌△CEF,
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)解:由(1)知:△DEF是等腰三角形,DE=EF,
由(2)知,∠DEF=∠B,
而∠B不可能为直角,
∴△DEF不可能是等腰直角三角形.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.下列关于$\sqrt{5}$的叙述,错误的是( )
| A. | $\sqrt{5}$是有理数 | B. | 面积为5的正方形边长是$\sqrt{5}$ | ||
| C. | $\sqrt{5}$介于2和3之间 | D. | 在数轴上可以找到表示$\sqrt{5}$的点 |
17.已知点D与点A(0,8),B(0,-2),C(x,y)是平行四边形的四个顶点,其中x,y满足x-y+6=0,则CD长的最小值为( )
| A. | $\frac{16}{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 10 |
 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F,已知BD=2,设AD=x,CF=y,求y关于x的函数解析式.
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F,已知BD=2,设AD=x,CF=y,求y关于x的函数解析式.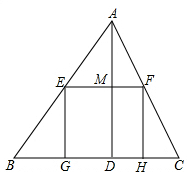 △ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一边GH在BC上,其余两个顶点E、F在AB,AC上,
△ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一边GH在BC上,其余两个顶点E、F在AB,AC上,


