题目内容
7.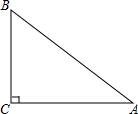 如图,已知△ABC中,∠ACB=90°,BC=6cm,AC=8cm.
如图,已知△ABC中,∠ACB=90°,BC=6cm,AC=8cm.(1)用直尺和圆规按下列要求作图:(保留作图痕迹,不写作法)作线段AB的垂直平分线,分别交AB、AC于点D、E.连接CD.
(2)试求CD和AE的长.
分析 (1)直接利用线段垂直平分线的作法得出AB的垂直平分线;
(2)利用线段垂直平分线的性质结合勾股定理以及相似三角形的判定与性质得出答案.
解答 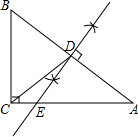 解:(1)如图所示:直线DE即为所求;
解:(1)如图所示:直线DE即为所求;
(2)∵直线DE垂直平分AB,
∴D是AB的中点,
∵∠ACB=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∴CD=$\frac{1}{2}$×AB=5(cm),
∵∠A=∠A,∠ADE=∠ACB,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$,
则$\frac{5}{8}$=$\frac{AE}{10}$,
解得:AE=$\frac{25}{4}$(cm),
答:CD的长为5cm,AE的长为$\frac{25}{4}$cm.
点评 此题主要考查了基本作图以及相似三角形的判定与性质,得出△ADE∽△ACB是解题关键.

练习册系列答案
相关题目
15.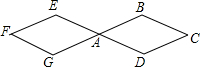 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )| A. | 点F | B. | 点G | C. | 点A | D. | 点C |
12.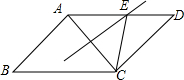 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )| A. | 6 | B. | 8 | C. | 14 | D. | 16 |
19.下列图形中,旋转60°后可以和原图形重合的是( )
| A. | 正六边形 | B. | 正方形 | C. | 正五边形 | D. | 正三角形 |