题目内容
2. 如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG、FG,判断四边形DEGF是怎样的四边形,并说明理由.
分析 (1)证明△DAE≌△DCF,根据全等三角形的性质证明;
(2)根据全等三角形的性质得到DE=DF,证明DG是EF的垂直平分线,得到DE=EG=GF=GF,证明结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
在△DAE和△DCF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{DA=DC}\\{∠A=∠C}\end{array}\right.$,
∴△DAE≌△DCF,
∴AE=CF;
(2)四边形DEGF是菱形,
∵△DAE≌△DCF,
∴DE=DF,
∵AE=CF,
∴BE=BF,
∴DG是EF的垂直平分线,
∴GE=GF,
∵OG=OD,DG⊥EF,
∴ED=EG,
∴DE=EG=GF=GF,
∴四边形DEGF是菱形.
点评 本题考查的是正方形的性质、菱形的判定、全等三角形的判定和性质,掌握相关的性质定理和判定定理是解题的关键.

练习册系列答案
相关题目
 如图,在一幅扇形统计图中,扇形A所占的百分比是35%,则扇形A的圆心角是126°.
如图,在一幅扇形统计图中,扇形A所占的百分比是35%,则扇形A的圆心角是126°.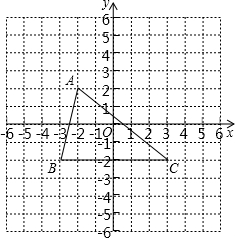 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度得△A1B1C1,解答下列各题.(每个小方格的边长为1个单位长度)
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度得△A1B1C1,解答下列各题.(每个小方格的边长为1个单位长度)