Question

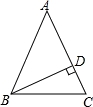
如图，在△ABC中，∠C=∠ABC=2∠A，BD⊥AC于D，求∠DBC的度数．

Answer 1

【考点】三角形内角和定理．

【分析】根据三角形的内角和定理与∠C=∠ABC=2∠A，即可求得△ABC三个内角的度数，再根据直角三角形的两个锐角互余求得∠DBC的度数．

【解答】解：∵∠C=∠ABC=2∠A，

∴∠C+∠ABC+∠A=5∠A=180°，

∴∠A=36°．

∴∠C=∠ABC=2∠A=72°．

∵BD⊥AC，

∴∠DBC=90°﹣∠C=18°．

【点评】本题考查的是等腰三角形的性质，解答此类题目时往往用到三角形的内角和是180°这一隐藏条件．