题目内容
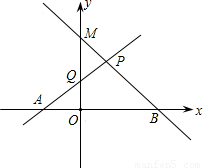
如图,已知直线PA是一次函数y=x+n (n>0)的图像,直线PB是一次函数y=-2x+m(m>n)的图像。
(1)用m,n表示A、B 、P点的坐标;
(2)若点Q是PA与y轴的交点,且四边形PQOB的面积是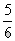 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。
(2)若点Q是PA与y轴的交点,且四边形PQOB的面积是
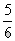 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。解:(1)A(-n,0), B(  ,0), P(
,0), P(  ,
, );
);
(2)连接PO,则依题意:m>0,n>0
SΔPOB= OB·|yp|=
OB·|yp|=  ·
· ·
·  =
=  ,
,
SΔPOQ= OQ·|xp|=
OQ·|xp|=  ·n·
·n· =
= ,
,
∵ S四边形PQOB=SΔPOB+ SΔPOQ = ,AB=2,
,AB=2,
∴ 解得:m=2, n=1.
解得:m=2, n=1.
故P点坐标为( ,
, ),直线PA的解析式是y=x+1,直线PB的解析式是y=-2x+2。
),直线PA的解析式是y=x+1,直线PB的解析式是y=-2x+2。
 ,0), P(
,0), P(  ,
, );
);(2)连接PO,则依题意:m>0,n>0
SΔPOB=
 OB·|yp|=
OB·|yp|=  ·
· ·
·  =
=  ,
, SΔPOQ=
 OQ·|xp|=
OQ·|xp|=  ·n·
·n· =
= ,
, ∵ S四边形PQOB=SΔPOB+ SΔPOQ =
 ,AB=2,
,AB=2, ∴
 解得:m=2, n=1.
解得:m=2, n=1. 故P点坐标为(
 ,
, ),直线PA的解析式是y=x+1,直线PB的解析式是y=-2x+2。
),直线PA的解析式是y=x+1,直线PB的解析式是y=-2x+2。
练习册系列答案
相关题目
 m>n)的图象.
m>n)的图象. 如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.
如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象. ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.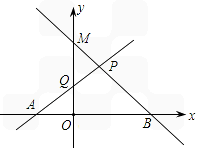
 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.