题目内容
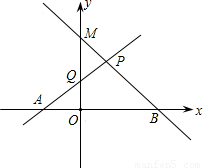
如图,已知直线PA是一次函数y=x+n (n>0)的图象,直线PB是一次函数y=-2x+m( m>n)的图象.
m>n)的图象.(1)用m,n表示A、B、P点的坐标;
(2)若点Q是PA与y轴的交点,且四边形PQOB的面积是
| 5 | 6 |
分析:二元一次方程组与一次函数的综合运用,再加上四边形的面积.首先根据一次函数求出点的坐标,求第(2)问时,设PB与y轴交于一点M,四边形面积等于三角形MOB的面积-三角形MQP的面积,从而得出结果.
解答: 解:(1)设A(a,0),B(b,0),P(x,y).
解:(1)设A(a,0),B(b,0),P(x,y).
由题意得:a+n=0①,-2b+m=0②,
由①②得a=-n,b=
.
解方程组
,
得
.
故A(-n,0),B(
,0),P(
,
);
(2)设PB与y轴交于一点M,则M(0,m),Q(0,n).
则SMOB=
m•
=
,SMQP=
•
• (m-n)=
.
所以
-
=
③,
又
+n=2 ④
③④联立,解得
.
∴点P的坐标为(
,
),直线PA的解析式为y=x+1,直线PB的解析式为y=-2x+2.
 解:(1)设A(a,0),B(b,0),P(x,y).
解:(1)设A(a,0),B(b,0),P(x,y).由题意得:a+n=0①,-2b+m=0②,
由①②得a=-n,b=
| m |
| 2 |
解方程组
|
得
|
故A(-n,0),B(
| m |
| 2 |
| m-n |
| 3 |
| m+2n |
| 3 |
(2)设PB与y轴交于一点M,则M(0,m),Q(0,n).
则SMOB=
| 1 |
| 2 |
| m |
| 2 |
| m2 |
| 4 |
| 1 |
| 2 |
| m-n |
| 3 |
| (m-n)2 |
| 6 |
所以
| m2 |
| 4 |
| (m-n)2 |
| 6 |
| 5 |
| 6 |
又
| m |
| 2 |
③④联立,解得
|
∴点P的坐标为(
| 1 |
| 3 |
| 4 |
| 3 |
点评:二元一次方程组与一次函数的综合运用,再加上四边形的面积.求解时很容易出错,一定要认真的练习.求四边形面积要学会运用整体思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.
如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.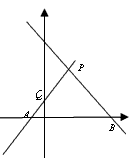
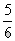 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.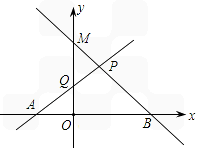
 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.