题目内容
5.计算下列各题:(1)6sin230°-$\sqrt{3}$cos30°-2sin45°;
(2)已知a=sin45°,b=sin60°,求$\frac{{a}^{2}+ab}{{a}^{2}+2ab+{b}^{2}}$-(a-b)2÷$\frac{({a}^{2}-{b}^{2})}{b}$.
分析 (1)把对应的特殊角的三角函数值代入化简计算.
(2)根据已知和特殊角的三角函数值求得a+b=$\frac{\sqrt{2}+\sqrt{3}}{2}$,a-b=$\frac{\sqrt{2}-\sqrt{3}}{2}$,代入化简后的分式计算.
解答 解:(1)原式=6×($\frac{1}{2}$)2-$\sqrt{3}$×$\frac{\sqrt{3}}{2}$-2×$\frac{\sqrt{2}}{2}$
=-$\sqrt{2}$.
(2)$\frac{{a}^{2}+ab}{{a}^{2}+2ab+{b}^{2}}$-(a-b)÷$\frac{({a}^{2}-{b}^{2})}{b}$
=$\frac{a(a+b)}{(a+b)^{2}}$-(a-b)×$\frac{b}{(a+b)(a-b)}$
=$\frac{a}{a+b}$-$\frac{b}{a+b}$=$\frac{a-b}{a+b}$.
∵a=sin45°=$\frac{\sqrt{2}}{2}$,b=sin60°=$\frac{\sqrt{3}}{2}$,
∴a+b=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{3}}{2}$,a-b=$\frac{\sqrt{2}-\sqrt{3}}{2}$
∴原式=$\frac{\frac{\sqrt{2}-\sqrt{3}}{2}}{\frac{\sqrt{2}+\sqrt{3}}{2}}$=2$\sqrt{6}$-5.
点评 考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现.解题关键是熟记特殊角的三角函数值.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.投掷一枚质地均匀的正方体骰子600次,朝上一面的点数为3的次数大约是( )
| A. | 100次 | B. | 200次 | C. | 300次 | D. | 400次 |
10.计算2n+2•(-2)•(2n)2的结果为( )
| A. | -62n+1 | B. | -23n+2 | C. | -23n+3 | D. | -82n+3 |
14.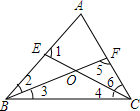 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )| A. | ∠BOC=∠2+∠6+∠A | B. | ∠2=∠5-∠A | C. | ∠5=∠1+∠A | D. | ∠1=∠ABC+∠4 |
 如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两边长分别为3和5,则小正方形的面积为1或4.
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两边长分别为3和5,则小正方形的面积为1或4.