题目内容
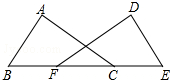 点B、F、C、E在同一直线上,且BF=CE,∠B=∠E.请你只添加一个边相等或角相等的条件(不再加辅助线),使△ABC≌△DEF.你添加的条件是:
点B、F、C、E在同一直线上,且BF=CE,∠B=∠E.请你只添加一个边相等或角相等的条件(不再加辅助线),使△ABC≌△DEF.你添加的条件是:考点:全等三角形的判定
专题:开放型
分析:此题是一道开放型的题目,答案不唯一,如∠A=∠D,理由是:求出BC=EF,根据AAS推出两三角形全等即可.
解答:解:∠A=∠D,
理由是:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF,
故答案为:∠A=∠D.
理由是:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
在△ABC和△DEF中
|
∴△ABC≌△DEF,
故答案为:∠A=∠D.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
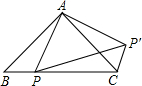 如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=
如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′= 点C是圆O直径AB上一点,过C点作弦DE,使CD等于CO,若弧AD的度数为40度,求弧BE的度数.
点C是圆O直径AB上一点,过C点作弦DE,使CD等于CO,若弧AD的度数为40度,求弧BE的度数. 如图,∠ABC=∠DCB=90°,E,F为BC上两点,且BE=CF,AB=DC.求证:△ABF≌△DCE.
如图,∠ABC=∠DCB=90°,E,F为BC上两点,且BE=CF,AB=DC.求证:△ABF≌△DCE.