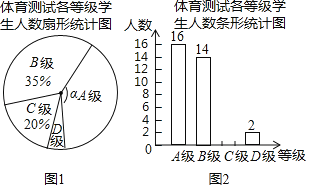
题目内容
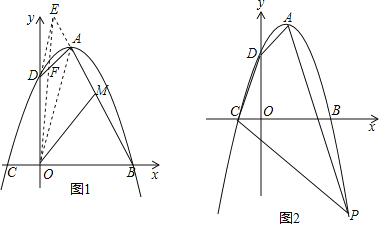
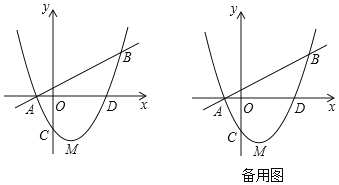
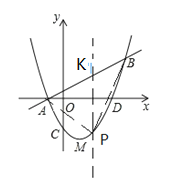
【题目】如图已知直线![]() 与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣
与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣![]() ),交x轴正半轴于D点,抛物线的顶点为M.
),交x轴正半轴于D点,抛物线的顶点为M.
(1)求抛物线的解析式;
(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;
(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,P(
,P(![]() ,
,![]() );(3)N(3,0)或N(2+
);(3)N(3,0)或N(2+![]() ,1+
,1+![]() )或N(5,6)或N(
)或N(5,6)或N(![]() ,1﹣
,1﹣![]() ).
).
【解析】
(1)将点![]() 代入
代入![]() ,求出
,求出![]() ,将点
,将点![]() 代入
代入![]() ,即可求函数解析式; (2)如图,过
,即可求函数解析式; (2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,求出
,求出![]() 的解析式,设
的解析式,设![]() ,表示
,表示![]() 点坐标,表示
点坐标,表示![]() 长度,利用
长度,利用![]() ,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设
,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设![]() ①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由
①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由![]() (AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点
(AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
解:(1)将点![]() 代入
代入![]() ,∴
,∴![]() ,
,
将点![]() 代入
代入![]() ,
,
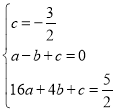 解得:
解得: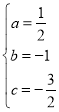 ,
,
∴函数解析式为![]() ;
;
(2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,设
,设![]() 为
为![]() ,
,
因为:![]() 所以:
所以:
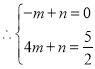 ,解得:
,解得: ,
,
所以直线AB为:![]() ,设
,设![]() ,则
,则![]() ,
,
所以:![]() ,
,
所以:![]()
![]() ,
,
当![]() ,
,![]() ,
,
此时:![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
∴△MAD是等腰直角三角形.
∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,
设![]()
①如图1,当MQ⊥QN时,此时![]() 与
与![]() 重合,N(3,0);
重合,N(3,0);
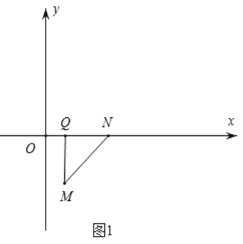
②如图2,当QN⊥MN时,过点N作NR⊥x轴于![]() ,过点M作MS⊥RN交于点S.
,过点M作MS⊥RN交于点S.
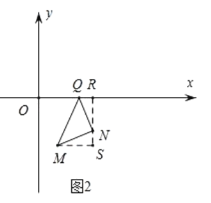
∵QN=MN,∠QNM=90°,∴![]() (AAS),
(AAS),![]()
∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过
R∥x轴,与过![]() 点的垂线分别交于点S、R;
点的垂线分别交于点S、R;
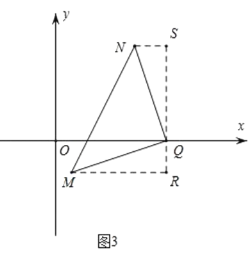
∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),![]() ,
,
![]() ,∴
,∴![]() ,∴t=5,(舍去负根)∴N(5,6);
,∴t=5,(舍去负根)∴N(5,6);
④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,
过点N作x轴的平行线,与两垂线交于点R、S;
∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,
∴![]() ,∴
,∴![]() .
.
![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
综上所述:![]() 或
或![]() 或N(5,6)或
或N(5,6)或![]() .
.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则![]() (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
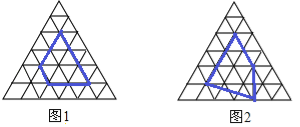
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).