题目内容
10.先观察下列的计算,再完成:$\frac{1}{{\sqrt{2}+1}}=\frac{{(\sqrt{2}-1)}}{{(\sqrt{2}+1)(\sqrt{2}-1)}}=\sqrt{2}-1$;$\frac{1}{{\sqrt{3}+\sqrt{2}}}=\frac{{(\sqrt{3}-\sqrt{2})}}{{(\sqrt{3}+\sqrt{2})(3-\sqrt{2})}}=\sqrt{3}-\sqrt{2}$;$\frac{1}{{\sqrt{4}+\sqrt{3}}}=\frac{{(\sqrt{4}-\sqrt{3})}}{{(4+3)(4-\sqrt{3})}}=\sqrt{4}-\sqrt{3}$;请你直接写出下面的结果:(1)$\frac{1}{{\sqrt{5}+\sqrt{4}}}$=$\sqrt{5}$-2;$\frac{1}{{\sqrt{6}+\sqrt{5}}}$=$\sqrt{6}$-$\sqrt{5}$;
(2)根据你的猜想、归纳,运用规律计算:$(\frac{1}{{1+\sqrt{2}}}+\frac{1}{{\sqrt{2}+\sqrt{3}}}+\frac{1}{{\sqrt{3}+\sqrt{4}}}+…+\frac{1}{{\sqrt{2013}+\sqrt{2014}}})×(\sqrt{2014}+1)$.
分析 (1)观察已知计算过程得出分母有理化规律,将各式化简即可;
(2)原式分母有理化变形后,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{\sqrt{5}-\sqrt{4}}{(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})}$=$\sqrt{5}$-$\sqrt{4}$=$\sqrt{5}$-2;$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\frac{\sqrt{6}-\sqrt{5}}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\sqrt{6}$-$\sqrt{5}$;
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2014}$-$\sqrt{2013}$)×($\sqrt{2014}$+1)=($\sqrt{2014}$-1)×($\sqrt{2014}$+1)=2014-1=2013.
故答案为:(1)$\sqrt{5}$-2;$\sqrt{6}$-$\sqrt{5}$
点评 此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
5.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{21}$ |
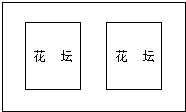 某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?
某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?