题目内容
14.在△ABC中,∠C=90°,AC=1,BC=2,M是AB的中点,以点C为圆心,1为半径作⊙C,则( )| A. | 点M在⊙C外 | B. | 点M在⊙C上 | C. | 点M在⊙C内 | D. | 不能确定 |
分析 根据题意画出图形,由勾股定理求出AB的长,再由直角三角形的性质得出OM的长,再与⊙C的半径相比较即可.
解答  解:如图,
解:如图,
∵在△ABC中,∠C=90°,AC=1,BC=2,
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
∵M是AB的中点,
∴CM=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$>1,
∴点M在⊙C外.
故选A.
点评 本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列四个式子中,计算结果最小的是( )
| A. | (-3-2)2 | B. | (-3)×(-2)2 | C. | -32÷(-2)2 | D. | -23-32 |
3.两次连续掷一枚质地均匀的色子,点数都是2朝上的概率是( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{2}$ |
 如图,过A、B、C三点作⊙O(注:本题要保留作图痕迹).
如图,过A、B、C三点作⊙O(注:本题要保留作图痕迹). 已知:如图,AB=DC,AC=DB,AB、CD交于点O.求证:∠A=∠D.
已知:如图,AB=DC,AC=DB,AB、CD交于点O.求证:∠A=∠D.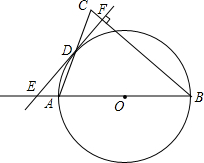 如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE 垂直BC于F,且交BA的延长线于点E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE 垂直BC于F,且交BA的延长线于点E.