题目内容
12.抛物线y=-3x2-2x+m与x轴交于A、B两点,P为顶点.(1)当△PAB为Rt△时,求m的值;
(2)当△PAB为等边三角形时,求m的值,你能得到什么结论吗?
分析 由抛物线与x轴的交点得出判别式>0,得出m的取值范围,再求出A、B、P的坐标;
(1)根据等腰直角三角形的性质得出方程,解方程即可;
(2)根据等边三角形的性质得出方程,解方程即可.
解答 解:∵抛物线与x轴有两个交点,
∴△=(-2)2-4×(-3)×m=4+12m>0,
解得:m>-$\frac{1}{3}$,
由题意得:P的坐标是(-$\frac{1}{3}$,$\frac{3m+1}{3}$)
A的坐标是($\frac{-2-\sqrt{4+12m}}{6}$,0),B的坐标是($\frac{-2+\sqrt{4+12m}}{6}$,0);
(1)当△PAB时直角三角形时,如图1所示:
根据题意得:-$\frac{1}{3}$-$\frac{-2-\sqrt{4+12m}}{6}$=$\frac{3m+1}{3}$,
解得:m=0或m=-$\frac{1}{3}$(不合题意,舍去),
故m=0;
(2)当△PAB为等边三角形时,如图2所示:
根据题意得:-$\frac{1}{3}$-$\frac{-2-\sqrt{4+12m}}{6}$=$\sqrt{3}$×$\frac{3m+1}{3}$,
解得:m=-$\frac{1}{3}$(不合题意,舍去),或m=-$\frac{2}{9}$,
∴m=-$\frac{2}{9}$.
点评 本题考查了抛物线与x轴的交点坐标、根的判别式、等腰直角三角形的性质、等边三角形的性质;本题有一定难度,需要画出图形,根据题意得出方程才能得出结果.

练习册系列答案
相关题目
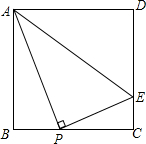 如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.
如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.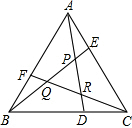 △ABC为正三角形,D、E、F三等分BC、AC、AB.如图,则S△PQR:S△ABC=$\frac{1}{7}$.
△ABC为正三角形,D、E、F三等分BC、AC、AB.如图,则S△PQR:S△ABC=$\frac{1}{7}$. y24-2×
y24-2× =607.
=607.