题目内容
如下图,点A是抛物线C1: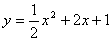 的顶点,点B是抛物线C2:
的顶点,点B是抛物线C2: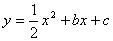 的顶点,并且OB⊥OA。
的顶点,并且OB⊥OA。
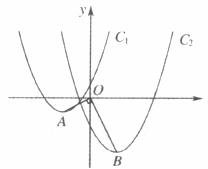

(1)求点A的坐标;
(2)若OB=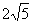 ,求抛物线C2的函数解析式;
,求抛物线C2的函数解析式;
(3)在(2)条件下,设P为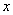 轴上的一个动点,探究:在抛物线C1或C2上是否存在点Q,使以点O,B,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由。
轴上的一个动点,探究:在抛物线C1或C2上是否存在点Q,使以点O,B,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由。
解:(1)A(-2,-1) (2分)
(2)以下为解题思路表述:
如图,作AD 轴于点D,BC
轴于点D,BC 轴于点C,
轴于点C,

由(1)得AD=1,OD=2,OA= ,
,
又由条件可推得△AOD∽△OBC, (证明相似,5分)
∴ ,即
,即
∴BC=4,同理可得OC=2, (7分)
∴B(2,-4), (8分)
∴抛物线C2:
即 (10分)
(10分)
(3)设Q( ),
),
如题图和备用图,在平行四边形中,

由于对角线平分平行四边形,
∴ ,可得
,可得 或
或 ,
,
∴ 或-2或6,
或-2或6,
∴Q1( ,4),Q2(
,4),Q2( ,4),Q3(-2,4),Q4(6,4),
,4),Q3(-2,4),Q4(6,4),
共四种情况 (14分)

水果店总共筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),要求将余下资金全部用于采购水果并使得所购水果装满货车.问应该怎样安排进货才能使水果店在销售完这批水果后获利最多?此时最大销售利润为多少元?
| 水果名称 | 进货价(元/千克) | 销售价(元/千克) |
| 凤梨 | 10 | 19 |
| 芒果 | 26 | 36 |
| 荔枝 | 22 | 30 |
 ,则tan∠B=_______.
,则tan∠B=_______.
 ,过点A,C作直线
,过点A,C作直线
 B.90°
B.90°  C.105° D.125°
C.105° D.125° ,则以x,y的值为两边长的等腰三角形的周长是
,则以x,y的值为两边长的等腰三角形的周长是 B.
B. C.a
C.a D.
D.