ÌâÄ¿ÄÚÈÝ
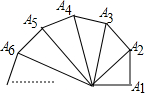 Èçͼ£¬ÒÑÖªÏ߶ÎOA1=1£¬¹ýµãA1×÷A1A2¡ÍOA1£¬ÇÒA1A2=1£¬Á¬½ÓOA2£¬ÔÙ¹ýµãA1×÷A2A3¡ÍOA2£¬ÇÒA2A3=1£¬Á¬½ÓOA3£¬Èç´Ë×÷³öÏ߶ÎA1A2=A2A3=¡=AnAn+1=1£¬Ò²µÃµ½ÁËnÌõÏ߶ÎOA1£¬OA2£¬OA3£¬¡OAn£®
Èçͼ£¬ÒÑÖªÏ߶ÎOA1=1£¬¹ýµãA1×÷A1A2¡ÍOA1£¬ÇÒA1A2=1£¬Á¬½ÓOA2£¬ÔÙ¹ýµãA1×÷A2A3¡ÍOA2£¬ÇÒA2A3=1£¬Á¬½ÓOA3£¬Èç´Ë×÷³öÏ߶ÎA1A2=A2A3=¡=AnAn+1=1£¬Ò²µÃµ½ÁËnÌõÏ߶ÎOA1£¬OA2£¬OA3£¬¡OAn£®²ÂÏëÓëÖ¤Ã÷£º
£¨1£©¼ÆËãOA2=
£¨2£©¸ù¾ÝÒÔÉϼÆË㣬Çë²ÂÏëOAnµÄ³¤¶È£¨Óú¬nµÄ´úÊýʽ±íʾ£©£¬²¢Ö¤Ã÷ÄãµÄ²ÂÏ룮
̽¾¿ÓëÖ¤Ã÷£º
£¨1£©ÀûÓÃÉÏÃæµÄ½áÂÛ£¬¿ÉµÃ£¬µ±OA1=A1A2=A2A3=¡AnAn+1=3ʱ£¬OAnµÄ³¤¶È£¨Óú¬nµÄ´úÊýʽ±íʾ£©Îª
£¨2£©ÈôOA1=A1A2=A2A3=¡=AnAn+1=aʱ£¬Çë²ÂÏëOAnµÄ³¤¶È£¨Óú¬a£¬nµÄ´úÊýʽ±íʾ£©£¬²¢Ö¤Ã÷ÄãµÄ²ÂÏ룮
¿¼µã£º¹´¹É¶¨Àí
רÌ⣺¹æÂÉÐÍ
·ÖÎö£º²ÂÏëÓëÖ¤Ã÷£º
£¨1£©ÔËÓù´¹É¶¨ÀíÖ±½Ó¼ÆË㣬¼´¿É½â¾öÎÊÌ⣮
£¨2£©Àà±È£¨1£©ÖеĽáÂÛ£¬¿ÉÒԲ²⣺OAn=
£»Ê×ÏÈÖ¤Ã÷OAn-1=
£¬½ø¶øµÃµ½OAn=
=
=
£®
̽¾¿ÓëÖ¤Ã÷£º
£¨1£©OAn=3
£®
£¨2£©²Â²â£ºOAnµÄ³¤¶È=a
£®Ê×ÏÈÖ¤Ã÷£ºOAn-12=(n-1)a2£¬ÔËÓù´¹É¶¨ÀíµÃµ½OAn2=(n-1)a2+a2
=na2£¬¼´¿É½â¾öÎÊÌ⣮
£¨1£©ÔËÓù´¹É¶¨ÀíÖ±½Ó¼ÆË㣬¼´¿É½â¾öÎÊÌ⣮
£¨2£©Àà±È£¨1£©ÖеĽáÂÛ£¬¿ÉÒԲ²⣺OAn=
| n |
| n-1 |
(
|
| n-1+1 |
| n |
̽¾¿ÓëÖ¤Ã÷£º
£¨1£©OAn=3
| n |
£¨2£©²Â²â£ºOAnµÄ³¤¶È=a
| n |
=na2£¬¼´¿É½â¾öÎÊÌ⣮
½â´ð£º
 ½â£º²ÂÏëÓëÖ¤Ã÷£º
½â£º²ÂÏëÓëÖ¤Ã÷£º
£¨1£©¸ù¾Ý¹´¹É¶¨ÀíµÃ£ºOA2=
=
£»OA3=
=
£»OA4=
=2£»
¹Ê´ð°¸Îª£º
£»
£»2£®
£¨2£©²ÂÏëOAn=
£»¹Ê´ð°¸Îª
£®
Ö¤Ã÷ÈçÏ£ºÓÉÌâÒâµÃ£¬OAn-1=
£¬
¹ÊOAn=
=
=
£®
̽¾¿ÓëÖ¤Ã÷£º
£¨1£©µ±OA1=A1A2=A2A3=¡AnAn+1=3ʱ£¬OAn=3
£¬
¹Ê´ð°¸Îª3
£®
£¨2£©µ±OA1=A1A2=A2A3=¡=AnAn+1=aʱ£¬Çë²ÂÏëOAnµÄ³¤¶È=a
£®
Ö¤Ã÷£º¡ßOAn-12=(n-1)a2£¬
¡àOAn2=(n-1)a2+a2=na2£¬
¡àOAn=a
£®
 ½â£º²ÂÏëÓëÖ¤Ã÷£º
½â£º²ÂÏëÓëÖ¤Ã÷£º£¨1£©¸ù¾Ý¹´¹É¶¨ÀíµÃ£ºOA2=
| 12+12 |
| 2 |
(
|
| 3 |
(
|
¹Ê´ð°¸Îª£º
| 2 |
| 3 |
£¨2£©²ÂÏëOAn=
| n |
| n |
Ö¤Ã÷ÈçÏ£ºÓÉÌâÒâµÃ£¬OAn-1=
| n-1 |
¹ÊOAn=
(
|
| n-1+1 |
| n |
̽¾¿ÓëÖ¤Ã÷£º
£¨1£©µ±OA1=A1A2=A2A3=¡AnAn+1=3ʱ£¬OAn=3
| n |
¹Ê´ð°¸Îª3
| n |
£¨2£©µ±OA1=A1A2=A2A3=¡=AnAn+1=aʱ£¬Çë²ÂÏëOAnµÄ³¤¶È=a
| n |
Ö¤Ã÷£º¡ßOAn-12=(n-1)a2£¬
¡àOAn2=(n-1)a2+a2=na2£¬
¡àOAn=a
| n |
µãÆÀ£º¸ÃÌâÖ÷Òª¿¼²éÁ˹´¹É¶¨Àí¼°ÆäÓ¦ÓÃÎÊÌ⣻½âÌâµÄ¹Ø¼üÊÇÀιÌÕÆÎÕ¹´¹É¶¨ÀíµÄÄÚÈÝ£¬Áé»îÔËÓù´¹É¶¨ÀíÀ´½âÌ⣮

Á·Ï°²áϵÁдð°¸
 СÌì²Å¿Îʱ×÷ҵϵÁдð°¸
СÌì²Å¿Îʱ×÷ҵϵÁдð°¸ Ò»¿ÎËÄÁ·ÏµÁдð°¸
Ò»¿ÎËÄÁ·ÏµÁдð°¸ »Æ¸ÔС״ԪÂú·Ö³å´Ì΢²âÑéϵÁдð°¸
»Æ¸ÔС״ԪÂú·Ö³å´Ì΢²âÑéϵÁдð°¸ и¨½Ìµ¼Ñ§ÏµÁдð°¸
и¨½Ìµ¼Ñ§ÏµÁдð°¸ Ñô¹âͬѧһÏßÃûʦȫÓźþíϵÁдð°¸
Ñô¹âͬѧһÏßÃûʦȫÓźþíϵÁдð°¸
Ïà¹ØÌâÄ¿
ijסլСÇø6Ô·ÝËæ»ú³é²éÁ˸ÃСÇø6ÌìµÄÓÃË®Á¿£¨µ¥Î»£º¶Ö£©£¬½á¹û·Ö±ðÊÇ30¡¢34¡¢32¡¢37¡¢28¡¢31£®ÄÇô£¬ÇëÄã¹À¼Æ¸ÃСÇø6Ô·ݣ¨30Ì죩µÄ×ÜÓÃË®Á¿µÄ¶ÖÊýÔ¼ÊÇ£¨¡¡¡¡£©
| A¡¢960 | B¡¢192 |
| C¡¢5760 | D¡¢32 |
Èôa£¾b£¬ÇÒcΪʵÊý£¬Ôò£¨¡¡¡¡£©
| A¡¢ac£¾bc |
| B¡¢ac£¼bc |
| C¡¢ac2£¾bc2 |
| D¡¢ac2¡Ýbc2 |
Á½Ô²µÄ°ë¾¶·Ö±ðΪ3cmºÍ4cm£¬ÇÒÁ½Ô²µÄÔ²ÐľàΪ7cm£¬ÔòÕâÁ½Ô²µÄ¹«ÇÐÏßÌõÊý¹²ÓУ¨¡¡¡¡£©
| A¡¢1Ìõ | B¡¢2Ìõ | C¡¢3Ìõ | D¡¢4Ìõ |
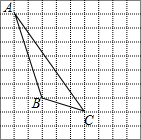 Èçͼ£¬ÔÚ·½¸ñÖ½ÄÚ½«¡÷ABCˮƽÏòÓÒƽÒÆ5¸öµ¥Î»µÃµ½¡÷A¡äB¡äC¡ä£®
Èçͼ£¬ÔÚ·½¸ñÖ½ÄÚ½«¡÷ABCˮƽÏòÓÒƽÒÆ5¸öµ¥Î»µÃµ½¡÷A¡äB¡äC¡ä£®
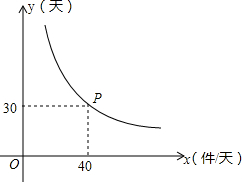 ÎÊÌâÇé¾³£ºÎªÁËÌá¸ß²úÆ·µÄ¼¼Êõº¬Á¿£¬ÎÒʡijóÒ×¹«Ë¾¼Æ»®°ÑÑз¢µÄÒ»ÅúвúÆ·¾«¼Ó¹¤ºóÔÙͶ·ÅÊг¡£¬¼Ó¹¤ËùÐèʱ¼äy£¨µ¥Î»£ºÌ죩Óëƽ¾ùÿÌìµÄ¹¤×÷Á¿x£¨µ¥Î»£º¼þ/Ì죩֮¼äµÄ¹ØϵÊÇÎÒÃÇѧ¹ýµÄijÖÖº¯Êý£¬ÆäͼÏóÈçͼËùʾ£®
ÎÊÌâÇé¾³£ºÎªÁËÌá¸ß²úÆ·µÄ¼¼Êõº¬Á¿£¬ÎÒʡijóÒ×¹«Ë¾¼Æ»®°ÑÑз¢µÄÒ»ÅúвúÆ·¾«¼Ó¹¤ºóÔÙͶ·ÅÊг¡£¬¼Ó¹¤ËùÐèʱ¼äy£¨µ¥Î»£ºÌ죩Óëƽ¾ùÿÌìµÄ¹¤×÷Á¿x£¨µ¥Î»£º¼þ/Ì죩֮¼äµÄ¹ØϵÊÇÎÒÃÇѧ¹ýµÄijÖÖº¯Êý£¬ÆäͼÏóÈçͼËùʾ£®