题目内容
14.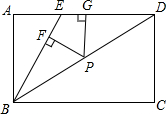 如图,E为矩形ABCD边AD上的一点,BE=ED,P为对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,且AB=2cm,求PF+PG=2.
如图,E为矩形ABCD边AD上的一点,BE=ED,P为对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,且AB=2cm,求PF+PG=2.
分析 连接PE,把△BED分成△BEP和△DEP两个三角形,然后利用三角形的面积列式进行计算即可得证.
解答 解:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP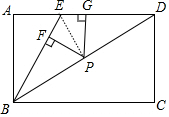
=$\frac{1}{2}$BE•PF+$\frac{1}{2}$ED•PG
=$\frac{1}{2}$ED•(PF+PG),
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=$\frac{1}{2}$ED•AB,
∴$\frac{1}{2}$ED•(PF+PG)=$\frac{1}{2}$ED•AB,
∴PF+PG=AB=2.
故答案为2.
点评 本题考查了矩形的性质,三角形的面积,解题的关键是学会添加常用作辅助线,利用三角形的面积的两种表示方法证明.

练习册系列答案
相关题目
17.下列四个几何体的俯视图中与众不同的是( )
| A. |  | B. |  | C. |  | D. |  |
9.-9的绝对值是( )
| A. | 9 | B. | -9 | C. | 3 | D. | -3 |
4.某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
| A. | 1月和11月 | B. | 1月、11月和12月 | C. | 1月 | D. | 1月至11月 |
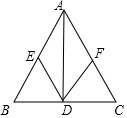 如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点. 如图所示,⊙I是Rt△ABC的内切圆,点D、E、F分别是且点,若∠ACB=90°,AB=5cm,BC=4cm,则⊙I的周长为2πcm.
如图所示,⊙I是Rt△ABC的内切圆,点D、E、F分别是且点,若∠ACB=90°,AB=5cm,BC=4cm,则⊙I的周长为2πcm.