题目内容
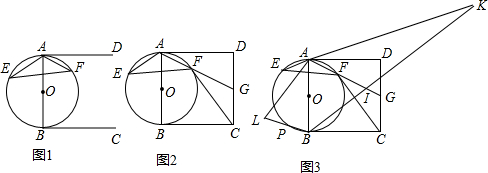
4.已知,AB是⊙O的直径,AE、AF是弦,BC是⊙O的切线,过点A作AD,使∠DAF=∠AEF.(1)如图(1),求证:AD∥BC;
(2)如图(2),若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若G为CD中点,求证:CF=CB;
(3)如图(3),在(2)的条件下,点I在线段FG上,且IF=AF,点P在$\widehat{BE}$上,连接BP并延长到L,使PL=PB,连接AL,延长EA、BI交于点K,已知∠BAK+∠ABL=180°,∠ABI+∠BAL=90°,⊙O的半径为$\frac{{\sqrt{10}}}{2}$,求四边形ALBK的面积.
分析 (1)连接BF,根据圆周角定理得到∠CBF=∠BAF,∠ABC=90°,等量代换得到∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,即可得到结论;
(2)连接BF,由(1)的结论推出四边形ABCD是正方形,得到tan∠DAG=$\frac{1}{2}$,设正方形ABCD的各边长为2a,求得tan∠ABF=$\frac{1}{2}$,根据勾股定理得到AG=$\sqrt{5}$a,求得tan∠CFG=$\frac{1}{2}$即可得到结论;
(3)连接AP,BF,由AB是⊙O的直径,得到AP⊥BL,根据AB是⊙O的直径,得到BP⊥AI,求得tan∠ABF=tan∠DAG=tan∠IBF=$\frac{1}{2}$,得到tan∠LAP=tan∠BAP=$\frac{1}{3}$,根据已知条件得到∠PAB=∠KAD,设BK与⊙O交于H,连接AH,过K作KK?⊥AB解三角形得到AH=$\frac{4\sqrt{10}}{5}$,BH=$\frac{3\sqrt{10}}{5}$,根据相似三角形的性质得到$\frac{AH}{KK′}$=$\frac{BH}{BK′}$,求得AK′=$\frac{4\sqrt{10}}{5}$,KK′=$\frac{12\sqrt{10}}{5}$,于是得到结论.
解答 解: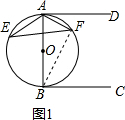 (1)连接BF,如图1所示:
(1)连接BF,如图1所示:
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠CBF=∠BAF,∠ABC=90°,
∵∠AEF=∠ABF,∠DAF=∠AEF,
∴∠ABF=∠DAF,
∴∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,
∴AD∥BC;
(2)如图2,连接BF,
由(1)知:∠BAD=∠ABC=90°,AD∥BC,
∵AD=BC=AB,
∴四边形ABCD是正方形,
∵G为CD中点,
∴tan∠DAG=$\frac{1}{2}$,
∵∠ABF=∠DAF,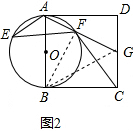
∴tan∠ABF=$\frac{1}{2}$,
∵∠BFG=∠BCD=90°,
∴B,C,G,F四点共圆,
∴∠CFG=∠CBG,
∵tan∠CBG=$\frac{CG}{BC}=\frac{1}{2}$,
∴tan∠CFG=$\frac{1}{2}$,
∴∠CFG=∠ABF,∠CFB=∠CBF,
∴CB=CF;
(3)如图3,连接AP,BF,
∵AB是⊙O的直径,
∴AP⊥BL,
∵LP=BP,
∴∠LAP=∠BAP,
∵AB是⊙O的直径,
∴BP⊥AI,
∵IF=AF,
∴∠ABF=∠IBF,
∴tan∠ABF=tan∠DAG=tan∠IBF=$\frac{1}{2}$,
又∵∠ABI+∠BAL=90°,
∴∠LAP+∠BAP=45°,
∴tan(∠LAP+∠BAP)=$\frac{tan∠LAP+tan∠BAP}{1-tan∠LAP•tan∠BAP}$=1,
tan∠LAP=tan∠BAP=$\frac{1}{3}$,
∵∠BAK+∠ABL=180°,
∴∠BAK+90°-∠PAB=180°,
∴∠BAK=90°+∠PAB,
又∴∠BAK=90°+∠KAD,
∴∠PAB=∠KAD,
设BK与⊙O交于H,连接AH,过K作KK?⊥AB,
∵tan∠ABF=$\frac{1}{2}$,AB=$\sqrt{10}$,
∴BF=AI=2$\sqrt{2}$,
∵AB=BI,
∴AH=$\frac{4\sqrt{10}}{5}$,BH=$\frac{3\sqrt{10}}{5}$,
∵△ABH∽△BKK′,
∴$\frac{AH}{KK′}$=$\frac{BH}{BK′}$,
∵KK′∥AD,
∴∠K′KA=∠DAK=∠BAP,
∴$\frac{AK′}{KK′}$=$\frac{1}{3}$,
∴AK′=$\frac{4\sqrt{10}}{5}$,
∴KK′=$\frac{12\sqrt{10}}{5}$,
∴S四边形ALBF=S△ALB+S△ABK=$\frac{1}{2}$BL•AP+$\frac{1}{2}$AB•KK′=3+12=15.
点评 本题考查了圆周角定理,相似三角形的判定和性质,平行线的性质,勾股定理,切线的性质,等腰三角形的性质,正确的作出辅助线构造相似三角形是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x2+x2+x2 | B. | x2•x2•x2 | C. | 3x•3x | D. | 9x |
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |

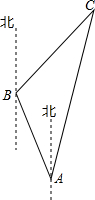 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)