题目内容
6.某电视机专卖店以2400元/台的价格进了一批的新上市的液晶电视机.平均每天售出50台,每台售价是3200元.为了增加知名度,专卖店决定采取适当的降价措施.经调查发现,如果每台液晶电视机每降价100元,平均每天可多售出5台.专卖店降价的第一天,获利36000元,则这天每台电视机降价多少元?分析 本题可设每台电视机降价x元,根据题中已知条件列出一台利润乘以销售量等于总利润的方程,解出答案即可.
解答 解:设每台电视机降价x元.
(3200-2400-x)×(50+x÷100×5)=36000,
整理得x2+200x-80000=0,
解得x1=200,x2=-400(舍去)
答:这天每台电视机降价200元.
点评 本题考查一元二次方程的实际运用,理解题意,找出降价和销售量的关系,以利润做为等量关系列方程求解.

练习册系列答案
相关题目
17.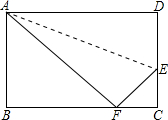 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
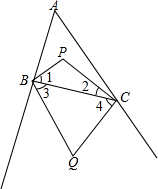 如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点.
如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点. 如图所示的一个魔方(正方体),每个面都是由9个面积为4cm2的小正方形拼成,求这个魔方的棱长.
如图所示的一个魔方(正方体),每个面都是由9个面积为4cm2的小正方形拼成,求这个魔方的棱长.