题目内容
11.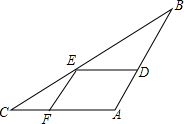 如图,△ABC中,DE∥AC,EF∥AB,∠BED=∠CEF,
如图,△ABC中,DE∥AC,EF∥AB,∠BED=∠CEF,(1)试说明△ABC是等腰三角形,
(2)探索AB+AC与四边形ADEF的周长关系.
分析 (1)由平行线的性质可得∠EAD=∠F,∠BAF=∠E,进而再通过角之间的转化得出结论;
(2)由平行线的性质可得∠EAD=∠F,∠BAF=∠E,由于∠BED=∠CEF,得到∠C=∠CEF=∠BED=∠B,于是得到EF=CF,DE=DB,即可得到结论.
解答 解:(1)∵DE∥AC
∴∠BED=∠C,
∵EF∥AB,
∴∠CEF=∠B,
∵∠BED=∠CEF,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)AB+AC=四边形ADEF的周长,
理由:∵DE∥AC,
∴∠BED=∠C,
∵EF∥AB,
∴∠CEF=∠B,
∵∠BED=∠CEF,
∴∠C=∠CEF=∠BED=∠B,
∴EF=CF,DE=DB,
∴AC+AB=CF+AF+AD+BD=EF+AF+AD+DE=四边形EFAD的周长.
点评 本题考查了平行线的性质,等腰三角形的判定与性质,熟练掌握各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算错误的是( )
| A. | a-2•a-1=a2 | B. | (a2)-3=a-6 | ||
| C. | a2÷a-3=a5 | D. | a-n=($\frac{1}{a}$)n(n为正整数) |
20.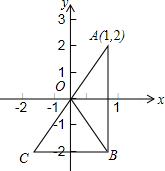 如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
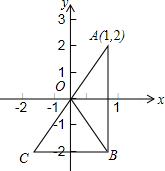 如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )| A. | (-1,-2) | B. | (1,-2) | C. | (-1,2) | D. | (-2,-1) |
 细心观察右图,认真分析下列各式,然后回答问题:
细心观察右图,认真分析下列各式,然后回答问题: 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.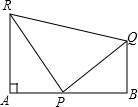 如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.
如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.