题目内容
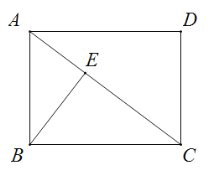
【题目】如图，已知点
是第一象限内横坐标为2的一个定点，
轴于点
，交直线
于点
，若点
是线段
上的一个动点，
，
，点在线段上运动时，点不变，
点随之运动，当点从点
运动到点时，则点运动的路径长是（ ）
A.
B.
C.2D.
【答案】D
【解析】
根据题意利用相似三角形可以证明线段
就是点
运动的路径（或轨迹），又利用
∽
求出线段的长度，即点B运动的路径长．
解：由题意可知，
，点
在直线
上，
轴于点
，
则
为顶角30度直角三角形，
.
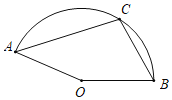
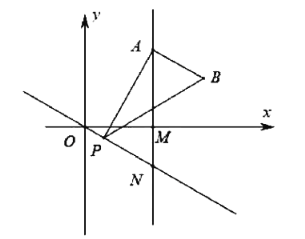
如下图所示，设动点
在
点（起点）时，点的位置为
，动点在点（终点）时，点的位置为
，连接，
∵
，
∴
又∵
，
∴
（此处也可用30°角的
）
∴∽，且相似比为
，
∴
现在来证明线段就是点运动的路径（或轨迹）.
如图所示，当点运动至
上的任一点时，设其对应的点为
，连接
，
，
∵，
∴
又∵，
∴
∴
∽
∴
又∵∽
∴
∴
∴点在线段上，即线段就是点运动的路径（或轨迹）.
综上所述，点运动的路径（或轨迹）是线段，其长度为
.
故选：
练习册系列答案
名校课堂系列答案
相关题目
