Question

【题目】有一个直径为2m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC．

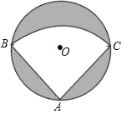
（1）求图中阴影部分的面积；

（2）若将扇形ABC围成一个圆锥，则该圆锥的底面半径最大是多少？

Answer 1

【答案】（1）；（2）

【解析】

（1）BC是圆O的直径，求出AC的值，进而利用扇形的面积公式可得阴影部分的面积；
（2）求出弧BC的长度，即圆锥底面圆的周长，继而可得出底面圆的半径．

解：（1）连接BC，AO，

∵∠BAC=90°，OB=OC，
∴BC是圆O的直径，AO⊥BC，
∵圆的直径为2，
∴AO=OC=1，
则AC=m，
故S扇形==πm2．
∴S阴影=π-π=π（m2）．
（2）弧BC的长l==πm，
则2πR=π，
解得：R=，

故该圆锥的底面圆的半径是m.