题目内容
15.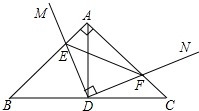 如图在Rt△ABC中,∠A=90°,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
如图在Rt△ABC中,∠A=90°,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①AE=CF;
②S四边形AEDF=$\frac{1}{2}$S△ABC;
③DE≤$\frac{1}{2}$AB;
④AD与EF可能互相垂直,其中正确结论的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 只要证明△AED≌△CFD可得①②正确,当DE⊥AB时,DE的值最小,DE的最小值=$\frac{1}{2}$AB,推出DE≥$\frac{1}{2}$AB,故③错误,当DE⊥AB时,四边形AEDF是正方形,此时EF与AD互相平分,故④正确,由此即可判断.
解答 解:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,
∵∠MDN=90°,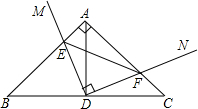
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
∵$\left\{\begin{array}{l}{∠EAD=∠C}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△AED≌△CFD(ASA),
∴AE=CF,故①正确,
∴S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=$\frac{1}{2}$S△ABC,故②正确,
∵当DE⊥AB时,DE的值最小,DE的最小值=$\frac{1}{2}$AB,
∴DE≥$\frac{1}{2}$AB,故③错误,
∵当DE⊥AB时,四边形AEDF是正方形,此时EF与AD互相平分,故④正确,
∴①②④正确,
故选B.
点评 本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,图形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.如图所示,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0)…,那么A2017的坐标为( )
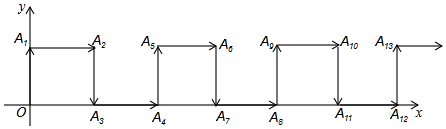

| A. | (2017,0) | B. | (1008,0) | C. | (1007,1) | D. | (1008,1) |
3.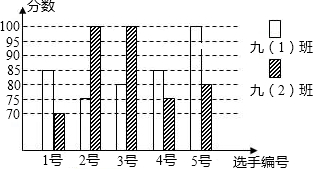 《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写表格;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
 《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.| 平均数 | 中位数 | 众数 | |
| 九(1)班 | 85 | 85 | |
| 九(2)班 | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
10.计算(14x3-21x2+7x)÷(-7x)的结果是( )
| A. | -x2+3x | B. | -2x2+3x-1 | C. | -2x2+3x+1 | D. | 2x2-3x+1 |
20. 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )
 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )| A. |  | B. |  | C. |  | D. |  |
 如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.
如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.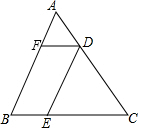 如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.
如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.