题目内容
6. 如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.
如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.
分析 答案不唯一,只要符合全等三角形的判定定理即可,如∠A=∠E或∠B=∠D或AB∥DE.
解答 解:∠A=∠E,
理由是:∵在△ABC和△EDF中
$\left\{\begin{array}{l}{∠1=∠2}\\{∠A=∠E}\\{AB=DE}\end{array}\right.$
∴△ABC≌△EDF(AAS),
故答案为:∠A=∠E.
点评 本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键.

练习册系列答案
相关题目
17. 如图所示,以O为端点的射线共有( )
如图所示,以O为端点的射线共有( )
 如图所示,以O为端点的射线共有( )
如图所示,以O为端点的射线共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
1.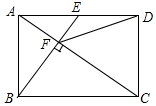 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
18. 如图,过直线外一点作已知直线的平行线,其依据是( )
如图,过直线外一点作已知直线的平行线,其依据是( )
 如图,过直线外一点作已知直线的平行线,其依据是( )
如图,过直线外一点作已知直线的平行线,其依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 两直线平行,同位角相等 | D. | 两直线平行,内错角相等 |
16.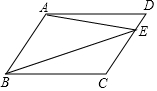 如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
 如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )| A. | 18° | B. | 21° | C. | 33° | D. | 45° |
 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的不等式kx+3>-x+b的解是x>2.
如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的不等式kx+3>-x+b的解是x>2.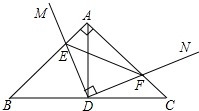 如图在Rt△ABC中,∠A=90°,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
如图在Rt△ABC中,∠A=90°,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论: