题目内容
19. 如图,在正方形ABCD中,AB=4,E,F分别是边BC,CD边上的动点,且AE=AF,设△AEF的面积为y,EC的长为x.
如图,在正方形ABCD中,AB=4,E,F分别是边BC,CD边上的动点,且AE=AF,设△AEF的面积为y,EC的长为x.(1)求y与x之间的函数表达式,并写出自变量x的取值范围.
(2)当x取何值时,△AEF的面积最大,最大面积是多少?
(3)在直角坐标系中画出y关于x的函数的图象.
分析 (1)根据正方形的性质可得AB=AD,再利用“HL”证明Rt△ABE和Rt△ADF全等,根据全等三角形对应边相等可得BE=DF,然后求出CE=CF,再根据△AEF的面积等于正方形的面积减去三个直角三角形的面积列式整理即可得解;
(2)结合(1)中二次函数解析式和x的取值范围来求△AEF的面积的最大值;
(3)利用(1)中二次函数解析式画出函数图象,注意x的取值范围.
解答 解:(1)在正方形ABCD中,AB=AD,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
∵CE=x,
∴BE=DF=4-x,
∴y=42-2×$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$x2,
=-$\frac{1}{2}$x2+4x,
即y=-$\frac{1}{2}$x2+4x.
∵E、F分别是BC、CD边上的动点,且保证A、E、F能构成三角形,
∴x的取值范围是:0≤x≤4;
(2)∵y=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8,0<x≤4,
∴当x=4时,△AEF的面积最大,最大面积是8;
(3)如图所示,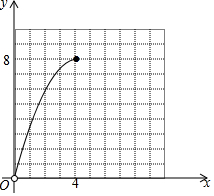
点评 本题考查了四边形综合题,涉及到了正方形的性质,全等三角形的判定与性质,三角形的面积以及二次函数最值的求法和二次函数图象,熟记性质并求出三角形全等是解题的关键.

练习册系列答案
相关题目
9.下面不是同类项的是( )
| A. | -2与12 | B. | -2a2b与a2b | C. | 2m与2n | D. | -x2y2与12x2y2 |
10.方程(x-1)(x+2)=0的解是( )
| A. | x1=1,x2=2 | B. | x1=-1,x2=2 | C. | x1=1,x2=-2 | D. | x1=-1,x2=-2 |
14. 有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
 有理数a,b在数轴上的位置如图,那么下列关系正确的是( )
有理数a,b在数轴上的位置如图,那么下列关系正确的是( )| A. | b>a | B. | -a>b | C. | |a|>|b| | D. | a>-b |
4.一组数据-1,2,3,4的极差是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.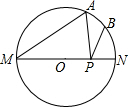 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 4 |
8.数25的算术平方根为( )
| A. | ±5 | B. | -5 | C. | 5 | D. | 25 |
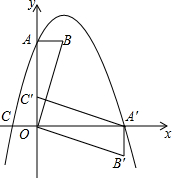 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.