题目内容
 如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?考点:等腰三角形的性质
专题:
分析:结合图形两周长的差就是腰长与底边的差,因为腰长与底边的大小不明确,所以分腰长大于底边和腰长小于底边两种情况讨论.
解答:解:根据题意结合图形,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
(2)若AB<BC,则BC-AB=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=6,BC=12,
6、6、12三边不能够组成三角形;
因此三角形的各边长为10、10、4.
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
(2)若AB<BC,则BC-AB=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=6,BC=12,
6、6、12三边不能够组成三角形;
因此三角形的各边长为10、10、4.
点评:本题主要考查等腰三角形的性质及三角形三边关系;做题中利用了分类讨论的思想,注意运用三角形三边关系对三角形的组成情况作出判断,这是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,已知:点D是△ABC的边BC上一动点,且AB=AC,DA=DE,∠BAC=∠ADE=α.
如图,已知:点D是△ABC的边BC上一动点,且AB=AC,DA=DE,∠BAC=∠ADE=α.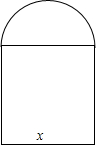 如图,隧道横截面的下部是矩形,上部是半圆,周长为20m.
如图,隧道横截面的下部是矩形,上部是半圆,周长为20m. 如图所示,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA=
如图所示,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA= 如图,在△ABC中,∠ABC的内角平分线延长后与∠ACB的外角平分线相交于点P.已知∠A=60°,则∠P等于
如图,在△ABC中,∠ABC的内角平分线延长后与∠ACB的外角平分线相交于点P.已知∠A=60°,则∠P等于