Question

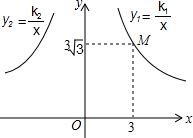如图，已知双曲线y₁=

k1

x

（x＞0）经过点M，它关于y轴对称的双曲线为y₂=

k2

x

(x＜0)．
（1）求双曲线y₁与y₂的解析式；
（2）若平行于x轴的直线交双曲线y₁于点A，交双曲线y₂于点B，在x轴上存在点P，使以点A，B，O，P为顶点的四边形是菱形，求点P的坐标．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）将点M的坐标代入双曲线y₁=

k1

x

（x＞0），求出k₁的值，从而得到y₁=

k1

x

（x＞0）的解析式，再根据对称性求出y₂的解析式；
（2）根据双曲线y₁与y₂关于y轴对称，求出OA=OB，设A(m，

9 3

m

)，则B(-m，

9 3

m

)，AB=2m，判断出△OAB是等边三角形，求出m的值，从而算出P点坐标．

解答：解：（1）∵M在双曲线y1=

k1

x

上，
将M（3，3

3

）代入y1=

k1

x

得，
∴

k

1

=9

3

，
∴y1=

9 3

x

(x＞0)，
∵双曲线y₁与y₂关于y轴对称，
∴y2=-

9 3

x

(x＜0)；
（2）∵双曲线y₁与y₂关于y轴对称，
∴点A与点B关于y轴对称，有OA=OB．
设A(m，

9 3

m

)，则B(-m，

9 3

m

)，AB=2m，
∵四边形OPAB是菱形，则OB=AB，
∴OA=AB=OB，
∴△OAB是等边三角形．
∴∠OAB=60°，
∴∠AOE=30°，
∴

9 3

m

=

3

m，
∴m=±3．
∵m＞0，
∴m=3，
∴P（6，0），
同理，当四边形OABP是菱形时，P（-6，0）；
综上所述，满足要求的点P有两个：P（6，0）或P（-6，0）．

点评：本题考查了反比例函数综合题，考查学生的猜想探究能力．解题时先直观地猜想，要注意数形结合，从直观到抽象．