题目内容
4.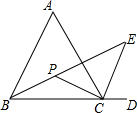 如图所示,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点P,延长BC到D,∠ACD的平分线交BP的延长线于点E,求∠BPC和∠E的度数.
如图所示,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点P,延长BC到D,∠ACD的平分线交BP的延长线于点E,求∠BPC和∠E的度数.
分析 根据三角形内角和定理和角平分线的性质得到∠BPC=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°,所以∠EPC=60°,再由CE是∠ACD的平分线,可证∠BCP=90°,进而可求出∠E的度数.
解答 解:∵在△ABC中∠A=60°,
∴∠ABC+∠ACB=120°.
∵BE是∠ABC的角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC.
又∵CP是∠ACB的平分线,
∴∠PCB=$\frac{1}{2}$∠ACB,
∴∠BPC=180°-∠PBC-∠PCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°,
∴∠EPC=60°,
∵CE是∠ACD的平分线,
∴∠BCP=$\frac{1}{2}$(∠BCA+∠ACD)=90°,
∴∠E=90°-60°=30°.
点评 本题考查三角形外角的性质及三角形的内角和定理,解题的关键是利用平角为180°以及角平分线的性质求得∠BCP=$\frac{1}{2}$(∠BCA+∠ACD)=90°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.贵阳数博会于2015年5月26日至29日在贵阳国际会议展览中心举行,贵阳副市长刘春成介绍在近两年签约投资额已经超过了1.4×103多亿元.1.4×103这个数可以表示为( )
| A. | 14 | B. | 140 | C. | 1400 | D. | 14000 |
19.已知ab>0,bc<0,化简:$\sqrt{-\frac{{a}^{3}{c}^{3}}{{b}^{3}}}$的结果为( )
| A. | $\frac{ac}{{b}^{2}}$$\sqrt{abc}$ | B. | $\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | C. | -$\frac{ac}{{b}^{2}}$$\sqrt{-abc}$ | D. | -$\frac{ac}{{b}^{2}}$$\sqrt{abc}$ |
 如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.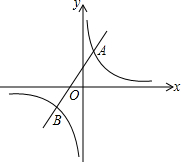 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)