题目内容
8.①计算:-12-|-3|+(-0.25)3×(-46)-(-5)0②先化简,后求值:当x、y满足x2+y2-2x+6y+10=0时,求代数式[(x-2y)2-(2x-y)(2x+y)-5y2]÷(-$\frac{1}{2}$x)的值.
分析 ①原式利用乘方的意义,绝对值的代数意义,零指数幂法则,以及积的乘方运算法则计算即可得到结果;
②已知等式整理后,利用非负数的性质求出x与y的值,原式化简后代入计算即可求出值.
解答 解:①原式=-1-3+64-1=59;
②原式=(x2-4xy+4y2-4x2+y2-5y2)÷(-$\frac{1}{2}$x)=(-3x2-4xy-y2)÷(-$\frac{1}{2}$x)=6x+8y+$\frac{2{y}^{2}}{x}$,
已知等式整理得:(x-1)2+(y+3)2=0,
可得x-1=0,y+3=0,
解得:x=1,y=-3,
则原式=6-24+18=0.
点评 此题考查了整式的混合运算-化简求值,实数的运算,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法中正确的是( )
| A. | 两数相加和为正数时,这两个数均为正数 | |
| B. | 两个数相加为负数时这两个数均为负数 | |
| C. | 互为相反数的两个数相加得零 | |
| D. | 在有理数加法中,两个数的和一定大于其中一个加数 |
19.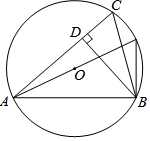 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
13.如图是从不同方向看某个几何体得到的图形,则这个几何体是( )


| A. | 正方体 | B. | 长方体 | C. | 圆柱 | D. | 球 |
20. 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )| A. | 180° | B. | 150° | C. | 120° | D. | 90° |
 小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.
小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.