题目内容
两个同心圆中,大圆的半径为8,小圆的半径为4,AB为大圆的弦,若AB=8
.请判断小圆与直线AB的位置关系,并给予证明.
| 3 |
考点:直线与圆的位置关系
专题:常规题型
分析:作OC⊥AB于C,连接OA,如图,根据垂径定理得到AC=
AB=4
,在Rt△AOC中理由勾股定理计算出OC=4,由于小圆的半径为4,则圆心O到直线AB的距离等于小圆的半径,然后根据直线与圆的位置关系的判定得到即可得到小圆与直线AB相切.
| 1 |
| 2 |
| 3 |
解答:解:小圆与直线AB相切.理由如下:
作OC⊥AB于C,连接OA,如图,
∵OC⊥AB,
∴AC=BC=
AB=
×8
=4
,
在Rt△AOC中,∵AC=4
,OA=8,
∴OC=
=4,
而小圆的半径为4,
∴圆心O到直线AB的距离等于小圆的半径,
∴小圆与直线AB相切.

作OC⊥AB于C,连接OA,如图,
∵OC⊥AB,
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△AOC中,∵AC=4
| 3 |
∴OC=
| OA2-AC2 |
而小圆的半径为4,
∴圆心O到直线AB的距离等于小圆的半径,
∴小圆与直线AB相切.
点评:本提考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 已知:在△ABC中,∠B=40°,∠C=20°,AD⊥AC交BC于点D,求证:CD=2AB.
已知:在△ABC中,∠B=40°,∠C=20°,AD⊥AC交BC于点D,求证:CD=2AB.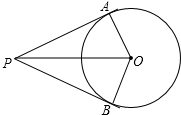 如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于
如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于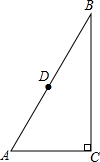 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断: