题目内容
18.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,…依此类推,那么第63个三角形数是2016.分析 根据所给的数据发现:第n个三角形数是1+2+3+…+n,由此代入分别求得答案即可.
解答 解:∵1+2=3,1+2+3=6,1+2+3+4=10,
∴由题意可得,第63个三角形数是:1+2+3+4+…+63=$\frac{64×63}{2}$=2016,
故答案为:2016.
点评 此题考查了数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
9.某市2016年参加中考的考生人数约为85000人,将85000用科学记数法表示为( )
| A. | 8.5×104 | B. | 8.5×105 | C. | 0.85×104 | D. | 0.85×105 |
3.函数y=$\sqrt{\frac{-1}{2-x}}$有意义的条件是( )
| A. | x≠2的实数 | B. | x<2的实数 | C. | x>2的实数 | D. | x>0且x≠2的实数 |
8.为庆祝元旦节,某幼儿园举行用火柴棒摆“金鱼”比赛,如图所示:
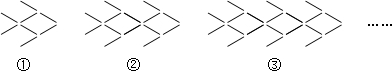
按照上面的规律,摆6条“金鱼”需用火柴棒的根数为( )
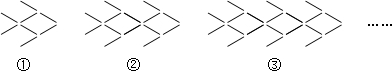
按照上面的规律,摆6条“金鱼”需用火柴棒的根数为( )
| A. | 48 | B. | 44 | C. | 38 | D. | 32 |
 已知二次函数y=(x-2)2-4.
已知二次函数y=(x-2)2-4.