题目内容
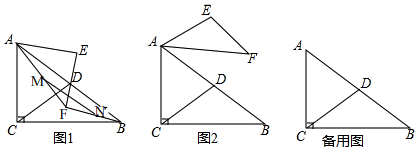
5．
如图，△ABC的中线BE、CF交于点O，直线AD∥BC，与CF的延长线交于点D，则S△AEF：S△AFD为（ ）| A． | 1：2 | B． | 3：2 | C． | 2：3 | D． | 3：4 |
分析 设△OEC的面积为s，利用三角形的中线的性质，找出三角形面积的关系，即可得出结论．
解答 解：
如图，连接AO，设△OEC的面积为s，
∵AF=BF，AE=EC，
∴EF∥BC，EF=$\frac{1}{2}$BC，
∴$\frac{EF}{BC}$=$\frac{1}{2}$，
∴S△EOC=S△AOE=s，S△AOF=S△AOC=s，
∴S△AFC=3s，
∵AD∥BC，
∴∠ADF=∠FCB，
在△ADF和△BCF中，
$\left\{\begin{array}{l}{∠ADF=∠BCF}\\{∠AFD=∠BFC}\\{AF=BF}\end{array}\right.$，
∴△ADF≌△BCF，
∴DF=CF，
∴S△AFD=S△AFC=3s，
∵AE=EC，
∴S△AFE=$\frac{1}{2}$S△AFC=$\frac{3}{2}$s，
∴S△AEF：S△AFD=$\frac{3}{2}$s：3s=1：2；
故选A．
点评 本题考查全等三角形的判定和性质、三角形中线的性质、三角形面积问题等知识，解题的关键理解中线把三角形分成面积相等的两部分，异底同高的两个三角形面积比等于底的比，属于中考常考题型．
练习册系列答案
计算高手系列答案
相关题目
如图，∠ADC=∠ABC=90°，AD=AB，E是AB上任意一点．求证：DE=BE．
已知：如图，AB=CD，AE⊥BC，DF⊥BC，CE=BF．
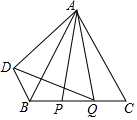如图，△ABC是等边三角形，AB=2cm，动点P、Q分别从点B、C同时出发，运动速度均为2cm/s．点P从B点出发，沿B→C运动，到点C停止，点Q从点C出发，沿C→B运动，到点B停止，连接AP、AQ，点P关于直线AB的对称点为D，连接BD、DQ，设点P的运动时间为t（s）．
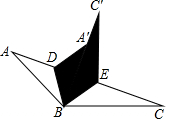如图所示，将一张三角形纸片分别沿着BD，BE对折，使点C落在点C′，点A落在点A′，点B，A′，C′在同一条直线上，若∠ABC=130°，则∠DBE=65度．