题目内容
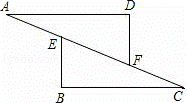
如图，在△ADF与△CBE中，点A，E，F，C在同一直线上，现给出下列四个论断：①AE=CF；②AD=CB；③∠B=∠D；④AD∥BC．请你选择其中三个作为条件，余下的一个作为结论，构成一个命题．请问：
（1）在所有构成的命题中有假命题吗？若有，请写出它的条件和结论（用序号表示）；若没有，请说明理由；
（2）在所有构成的真命题中，任意选择一个加以证明．
解：
（1）假命题为：条件①②③；结论④．
（2）（答案不唯一）
已知条件①③④；结论②
已知AE=CF，∠B=∠D，AD∥BC．
求证：AD=CB
证明：∵AE=CF，
∴AE+EF=CF+EF．
∴AF=EC．
∵AD∥BC，
∴∠A=∠C．
又∵∠B=∠D，
∴△ADF≌△EBC（AAS）．
∴AD=CB
．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
BC的长为半径作弧，两弧相交于M，N两点；
．
