题目内容
7．
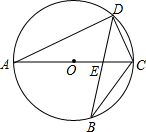如图，AC是⊙O的直径，弦BD交AC于点E．（1）求证：△ADE∽△BCE；
（2）如果AD=5，BC=3，CE=1，求DE的长．
分析 （1）根据圆周角定理，即可得到△ADE和△BCE中两组对应角相等，由此证得△ADE∽△BCE；
（2）由△ADE∽△BCE，得到$\frac{AD}{BC}=\frac{DE}{CE}$，即可得到结果．
解答 （1）证明：∵∠A=∠B，∠AED=∠BEC，
∴△ADE∽△BCE，
（2）∵△ADE∽△BCE，
∴$\frac{AD}{BC}=\frac{DE}{CE}$，
$即\frac{5}{3}=\frac{DE}{1}$，
∴$DE=\frac{5}{3}$．
点评 本题考查了相似三角形的判定和性质、圆周角的定理，熟记 定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
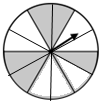如图，一个圆形转盘被分成12个圆心角都为30°的扇形，任意转动这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是$\frac{5}{12}$．
如图，一次函数y=kx+2的图形与反比例函数y=$\frac{m}{x}$的图象交于点P，点P在第一象限，PA⊥x轴于点A，一次函数的图象分别交x轴、y轴于点C、D，且S△COD=1，$\frac{CO}{OA}=\frac{1}{2}$．
如图，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，
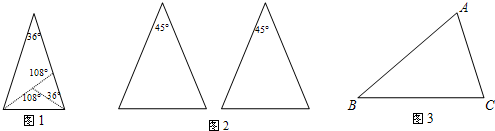
已知：如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点A出发，沿AB方向匀速运动，速度为1cm/s；过点P作直线PF∥AD，PF交CD于点F，过点F作EF⊥BD，且与AD、BD分别交于点E、Q；连接PE，设点P的运动时间为t（s）（0＜t＜10）．