题目内容
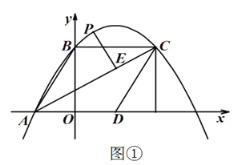
【题目】如图①,在半径为6的扇形AOB中,![]() ,点C是弧AB上的一个动点(不与点
,点C是弧AB上的一个动点(不与点![]() 、
、![]() 重合),
重合),![]() 、
、![]() ,垂足分别为D、E.
,垂足分别为D、E.
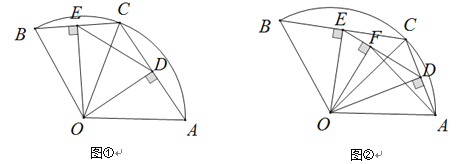
(1)①当![]() 时,线段
时,线段![]() ;
;
②当![]() 的度数= °时,四边形
的度数= °时,四边形![]() 成为菱形;
成为菱形;
(2)试说明:四边形![]() 的四个顶点在同一个圆上;
的四个顶点在同一个圆上;
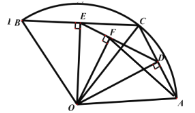
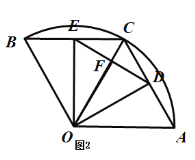
(3)如图②,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,随着点
,随着点![]() 的运动,在△
的运动,在△![]() 中是否存在保持不变的角?如果存在,请指出这个角并求出它的度数;如果不存在,请说明理由;
中是否存在保持不变的角?如果存在,请指出这个角并求出它的度数;如果不存在,请说明理由;
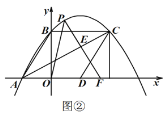
(4)在(3)条件下,若点![]() 从点
从点![]() 运动到点
运动到点![]() ,则点
,则点![]() 的运动路径长为 .
的运动路径长为 .
【答案】(1)①![]() ;②60;(2)证明见详解;(3)存在,
;②60;(2)证明见详解;(3)存在,![]() ;(4)3
;(4)3
【解析】
(1)①根据勾股定理即可求得线段![]() ;②点C为
;②点C为![]() 中点,即
中点,即![]() =60°时,得△OBC,△OAC为等边三角形,可得四边形
=60°时,得△OBC,△OAC为等边三角形,可得四边形![]() 成为菱形;
成为菱形;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,根据直角三角形斜边上的直线等于斜边的一半,证得
,根据直角三角形斜边上的直线等于斜边的一半,证得![]() ,问题得证;
,问题得证;
(3)先求得∠EOD=60°,根据(2)的结论,进行角的转化,证明∠EOF=∠AOD,进而求得![]() ;
;
(4)根据![]() 不变,确定
不变,确定![]() 的运动轨迹是一条线段,当点C与A、B重合时,OF最小,当C位于
的运动轨迹是一条线段,当点C与A、B重合时,OF最小,当C位于![]() 的中点时,OF最长,分别求出OF长,计算可得.
的中点时,OF最长,分别求出OF长,计算可得.
解:(1)①∵OB=OC, ![]() ,
,
∴BE=![]() ,
,
∴在Rt△OBE中,OE=![]() ;
;
故答案为:![]() ;
;
②当∠BOC=60°时,∠AOC=60°,△OBC,△OAC为等边三角形,
∴OA=AC=OC=BC=OB,
∴四边形![]() 成为菱形;
成为菱形;
故答案为:60;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]()
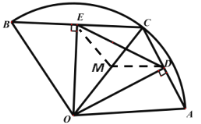
∵![]() ,
,![]() ∴
∴![]() ,
,![]()
∴![]()
∴以![]() 为圆心,
为圆心,![]() 为半径的圆过
为半径的圆过![]() 三点
三点
即四边形![]() 的四个顶点在同一个圆上
的四个顶点在同一个圆上
(3)答:![]() 不变,
不变,![]() ;
;
证明:∵OB=OC=OA, ![]() 、
、![]() ,
,
∴∠COE=∠BOE=![]() ,∠COD=∠AOD=
,∠COD=∠AOD=![]() ,
,
∴∠EOD=∠COE+∠COD=![]() ,
,
∵四边形![]() 的四个顶点在同一个圆上,
的四个顶点在同一个圆上,
∴![]() ,
,
∴∠OED=∠OCD,
∵OF⊥DE,OD⊥OC,
∴∠OEF+∠EOF=90°, ∠OCD+∠COD=90°,
∴∠EOF=∠COD,
∵∠COD=∠AOD,
∴∠EOF=∠AOD,
∴![]() ;
;
(4)由(3)得,![]() ,∴点F的运动轨迹在∠AOB的平分线上,
,∴点F的运动轨迹在∠AOB的平分线上,
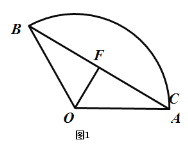
如图1,当点C与A重合时,F与E重合,∠OAB=30°,OF⊥AB,
∴OF=![]() ;
;
如图2,当点C运动到![]() 中点时,∠AOD=∠DOC=30°,
中点时,∠AOD=∠DOC=30°,
OD=OA·cos∠AOD=![]() ,
,
OF= OD·cos∠FOD=![]() ;
;
∴![]() ;
;
当点C从点B运动到![]() 中点时,也运动了
中点时,也运动了![]() ,
,
∴在(3)条件下,若点![]() 从点
从点![]() 运动到点
运动到点![]() ,则点
,则点![]() 的运动路径长为3.
的运动路径长为3.

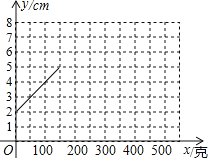
【题目】弹簧是一种利用弹性来工作的机械零件,用弹性材料制成的零件在外力作用下发生形变,除去外力后又恢复原状.某班同学在探究弹簧的长度与所受外力的变化关系时,通过实验记录得到的数据如下表:
砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
指针的位置y(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究,下面是小腾的探究过程,请补充完整.
(1)根据上述表格在平面直角坐标系中补全该函数的图象;
(2)根据画出的函数图象,写出:
①当x=0时,y= ,它的实际意义是 ;
②当指针的位置y不变时,砝码的质量x的取值范围为 .