题目内容
14.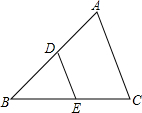 如图,△ABC中,∠B=50°,AB=BC,DE是中位线,则∠ADE=115°.
如图,△ABC中,∠B=50°,AB=BC,DE是中位线,则∠ADE=115°.
分析 由等腰三角形的性质:两个底角相等可求出∠A的度数,再根据三角形中位线定理可得DE∥AC,进而可求出∠ADE的度数.
解答 解:∵△ABC中,∠B=50°,AB=BC,
∴∠A=∠C=$\frac{180°-50°}{2}$=65°,
∵DE是中位线,
∴DE∥AC,
∴∠A+∠ADE=180°,
∴∠ADE=115°,
故答案为:115°.
点评 本题考查了三角形中位线定理、等腰三角形的性质以及平行线的性质,解题的关键是熟记三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.2015的相反数的倒数是( )
| A. | -$\frac{1}{2015}$ | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\sqrt{2015}$ |
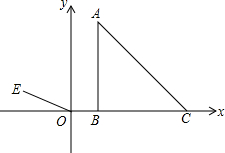 如图,在平面直角坐标系中,已知点E(-2,1),连结OE,△ABC的三个顶点坐标分别为A(1,4),B(1,0),C(5,0).
如图,在平面直角坐标系中,已知点E(-2,1),连结OE,△ABC的三个顶点坐标分别为A(1,4),B(1,0),C(5,0).
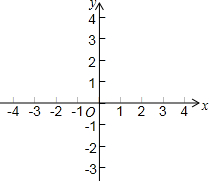 已知平面直角坐标系xOy(如图),双曲线y=$\frac{k}{x}$(k≠0)与直线y=x+2都经过点A(2,m).
已知平面直角坐标系xOy(如图),双曲线y=$\frac{k}{x}$(k≠0)与直线y=x+2都经过点A(2,m).