题目内容
1.解不等式组:$\left\{\begin{array}{l}{3(x+2)>x+4}\\{\frac{x}{4}≥\frac{x-1}{3}}\end{array}\right.$,并把它的解集在数轴上表示出来.分析 先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{3(x+2)>x+4①}\\{\frac{x}{4}≥\frac{x-1}{3}②}\end{array}\right.$
∵解不等式①得:x>-1,
解不等式②得:x≤4,
∴不等式组的解集为:-1<x≤4,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
9.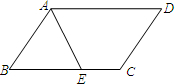 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.在下列手机软件图标中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.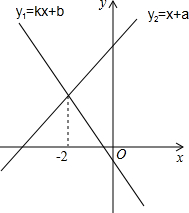 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )| A. | x>-2 | B. | x<-2 | C. | x≤-2 | D. | x≥-2 |
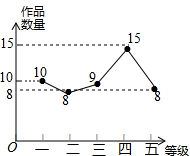 某校利用寒假进行科技实践活动,开学之初八(1)班对各组上交的“科技作品”的数量进行了统计,并绘制了如图的折线统计图.
某校利用寒假进行科技实践活动,开学之初八(1)班对各组上交的“科技作品”的数量进行了统计,并绘制了如图的折线统计图.