题目内容
如图，将面积为12的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中的四边形ACED的面积为考点：平移的性质
专题：
分析：先根据平移得出四边形ABED为平行四边形，再连接AE，由平移距离是边BC长的两倍，即BE=2BC=2CE即可得出结论．
解答：
解：∵△ABC沿着BC方向平移到△DEF的位置，
∴AB∥DE，AB=DE，
∴四边形ABED为平行四边形，
连接AE，
又∵平移距离是边BC长的两倍，即BE=2BC=2CE，
∴S△ABC=S△ACE，即S△ABE=2S△ABC，
又∵S△ABE=S△ADE，又S△ABC=12，
∴S四边形ACED=3S△ABC=36．
故答案为：36．．
解：∵△ABC沿着BC方向平移到△DEF的位置，∴AB∥DE，AB=DE，
∴四边形ABED为平行四边形，
连接AE，
又∵平移距离是边BC长的两倍，即BE=2BC=2CE，
∴S△ABC=S△ACE，即S△ABE=2S△ABC，
又∵S△ABE=S△ADE，又S△ABC=12，
∴S四边形ACED=3S△ABC=36．
故答案为：36．．
点评：本题考查的是平移的性质，熟知把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同是解答此题的关键．
练习册系列答案
精英口算卡系列答案
相关题目
如图，已知每个小正方形的边长为1cm，O、A、B都在小正方形顶点上，扇形OAB是某个圆锥的侧面展开图．这个圆锥的底面半径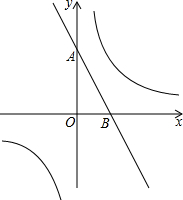
直线y=-2x+2与坐标轴交于A、B两点，在反比例函数y=