题目内容
16．
如图，在△ABC中，AB=AC，DE∥BC，∠A=40°，DC平分∠ACB，则∠EDC的度数为35°．
分析 根据等腰三角形的性质可求得∠ACB的度数，又由CD是∠ACB的平分线，求得∠BCD的度数，然后由DE∥BC，求得答案．
解答 解：∵AB=AC，
∴∠ACB=70°，
∵CD是∠ACB的平分线，
∴∠BCD=$\frac{1}{2}$∠ACB=35°，
∵DE∥BC，
∴∠EDC=∠BCD=35°．
故答案为：35．
点评 此题考查了等腰三角形的性质，平行线的性质以及三角形内角和定理．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
7．下列条件中不能确定菱形的形状和大小的是（ ）
| A． | 已知菱形的两条对角线 | B． | 已知菱形的一边和一个内角 | ||
| C． | 已知菱形的四边 | D． | 已知菱形的周长和面积 |
4．把圆柱的侧面沿高展开，得到的图形是（ ）
| A． | 长方形 | B． | 三角形 | C． | 长方形或正方形 |
8．当a为任意实数时，下列各式总有意义的是（ ）
| A． | $\sqrt{{a}^{2}}$ | B． | $\sqrt{a}$ | C． | $\sqrt{\frac{1}{{a}^{2}}}$ | D． | $\sqrt{-a}$ |
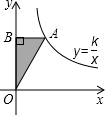如图，点A是反比例函数y=$\frac{k}{x}$（x≠0）的图象上一点，AB⊥y轴于B，若△ABO的面积为4，则k的值为8．