题目内容
10.已知一条直线y=kx+b经过点A(0,4)、点B(2,0).求:(1)直线的解析式;
(2)当x=-1时y的值;
(3)当x取何值时,y=2.
分析 (1)把A与B的坐标代入y=kx+b中,求出k与b的值,即可确定出直线解析式;
(2)把x=-1代入计算即可求出y的值;
(3)把y=2代入计算即可求出x的值.
解答 解:(1)把A(0,4)与B(2,0)代入y=kx+b中,得:$\left\{\begin{array}{l}{b=4}\\{2k+b=0}\end{array}\right.$,
解得:k=-2,b=4,
则直线解析式为y=-2x+4;
(2)把x=-1代入得:y=2+4=6;
(3)把y=2代入得:-2x+4=2,即x=1.
点评 此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
6.有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是( )
| A. | 如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根 | |
| B. | 如果方程M的两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
1.下列各式中,不能用平方差公式计算的是( )
| A. | (-2x-y)(2x-y) | B. | (-2x+y)(-2x-y) | C. | (2x+y)(-2x+y) | D. | (2x-y)(-2x+y) |
2.有一个三角形的两边是6cm和8cm,要使这个三角形为直角三角形,则第三边的长为( )
| A. | 10cm | B. | $2\sqrt{7}$cm | C. | 10cm或2$\sqrt{7}$cm | D. | 4cm |
19.下列语句中不是命题的是( )
| A. | 角是几何图形 | B. | 两平行线间的距离处处相等 | ||
| C. | 对顶角相等吗 | D. | 两个锐角的和是一个直角 |
 一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).
一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).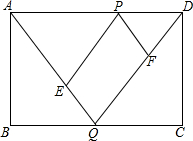 如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.
如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.