题目内容
解方程
（1）x（x+3）=7（x+3）；
（2）x2+5x-6=0．
（1）x（x+3）=7（x+3）；
（2）x2+5x-6=0．
考点：解一元二次方程-因式分解法
专题：计算题
分析：（1）方程变形后，提取公因式化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解；
（2）方程左边利用十字相乘法分解因式后，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
（2）方程左边利用十字相乘法分解因式后，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
解答：解：（1）方程变形得：x（x+3）-7（x+3）=0，
分解因式得：（x+3）（x-7）=0，
解得：x1=-3；x2=7；
（2）x2+5x-6=0
分解因式得：（x-1）（x+6）=0，
解得：x1=1；x2=-6．
分解因式得：（x+3）（x-7）=0，
解得：x1=-3；x2=7；
（2）x2+5x-6=0
分解因式得：（x-1）（x+6）=0，
解得：x1=1；x2=-6．
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
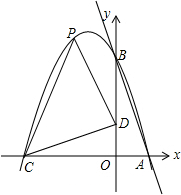如图，在直角坐标系中，直线y=-4x+4交坐标轴于点A、B，如图所示．将△AOB绕原点O逆时针旋转90°，得到△DOC．抛物线y=ax2+bx+c经过点A、B、C．
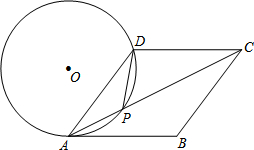如图，在菱形ABCD中，P是对角线AC上的一点，且PA=PD，⊙O为△APD的外接圆．
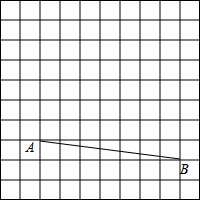在网格中每个小正方形的边长均为1，A、B两点在正方形的顶点上，
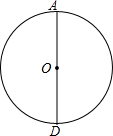在学习圆与正多边形时，马露、高静两位同学设计了一个画圆内接正三角形的方法：