题目内容
等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边
AB、AC交于点E、F.
（1）如图1，当点P为BC的三等分点，且PE⊥AB时，判断△EPF的形状；
（2）如图2，若点P在BC边上运动，且保持PE⊥AB，设BP=x，四边形AEPF面积的y，求y与x的函数关系式，并写出自变量x的取值范围；
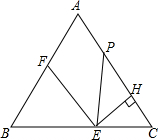
（3）如图3，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长.
（1）△EPF为等边三角形. --------------1分
（2）设BP=x，则CP＝6－x.
由题意可 △BEP的面积为.
△CFP的面积为.
△ABC的面积为.
设四边形AEPF的面积为y.
∴ =
.
自变量x的取值范围为3＜x＜6. --------------4分
（3）可证△EBP∽△PCF.
∴ .
设BP=x，
则 .
解得 .
∴ PE的长为4或. --------------7分
解析:略
练习册系列答案
相关题目
如图，等边△ABC边长为4，E是边BC上动点，EH⊥AC于H，过E作EF∥AC，交线段AB于点F，在线段AC上取点P，使PE=EB．设EC=x（0＜x≤2）．
7、如图，等边△ABC边长为3cm，将△ABC沿AC向右平移1cm，得到△DEF，则四边形ABEF的周长（ ）
14、如图，已知等边△ABC边长为1，D是△ABC外一点且∠BDC=120°，BD=CD，∠MDN=60°．
如图，等边△ABC边长为10cm，以AB为直径的⊙O分别交CA、CB于D、E两点，则图中阴影部分的面积（结果保留π）是